# 法拉第电磁感应定律
感应电动势:单位1V=1Wb/s
εi=−NdtdΦ
任一回路中:
Φ=∬SB⋅dS=∬SBcosθ⋅dS
从t1→t2 时间内,通过回路导线任一截面的感应电量:
q=∫t1t2Idt=−RN∫Φ1Φ2dΦ=−RN(Φ2−Φ1)
# 电源
提供非静电力,维持稳恒电流
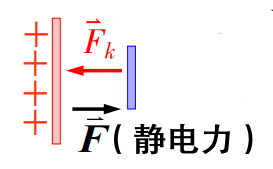
正电荷在静电场力的作用下从 A 经过导线移到 B,并与 B 上的负电荷中和,直至板间电势差消失。要维持稳恒电流,须使正电荷从 B 经 BA 内移至 A 上,使
两板间有恒定的电势差。
![]()
非静电场:
Ek=Fk/q
方向:电源内部由负极指向正极
电源电动势:单位正电荷从负极经电源内部移至正极时,非静电力做的功。
ε=qA=∫内部−内部+Ek⋅dl
# 感应电动势
# 动生电动势
导体在磁场中运动时产生的感应电动势
εi=vBL
Fk=−ev×B
Ek=v×B
# 感生电动势
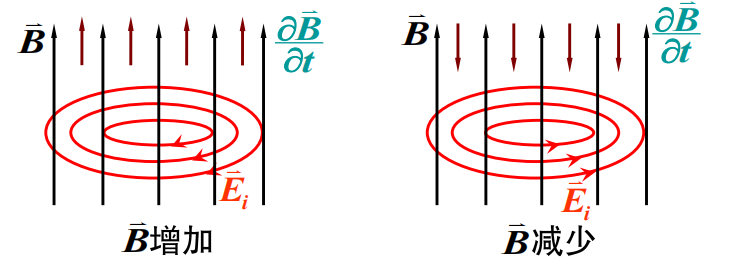
εi=−dtdΦ=−dtd∬SB⋅dS=−∬S∂t∂B⋅dS
考虑闭合回路:
![]()
∮LEi⋅dl=−∬S∂t∂B⋅dS
方向由楞次定律判断
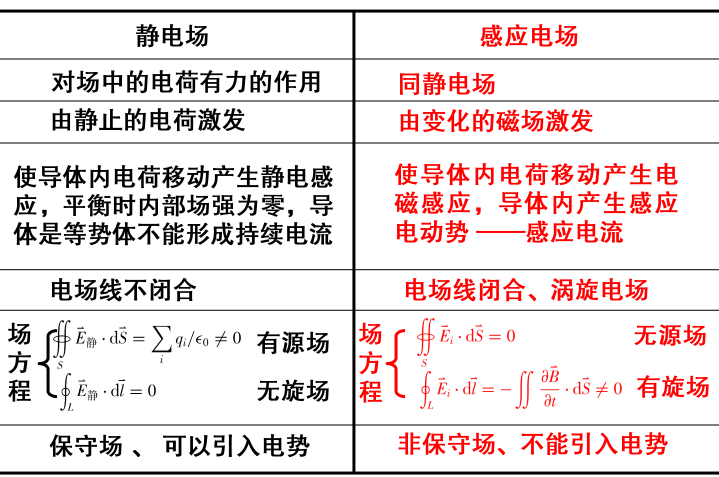
# 感应电场
感应电场是产生感应电动势的机制,不是静电场
E静为保守力场:
∮E静⋅dl=0
Ei 是非保守力场:
∮Ei⋅dl=0
![]()
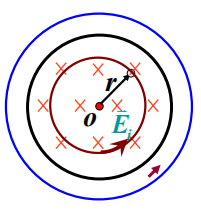
# 感应电场的计算
![]()
r<R时,Ei=−2r∂t∂B
r>R时,Ei=2rR2∂t∂B
Ei 是涡旋场–非保守场,不能引入势函数,但是它对在场中的导体提供电动势
导体不闭合时→ 使到体内电荷重新分布→ 产生E静→ 到体内总电场达到平衡→ 由于电荷的存在空间出现电势→ΔU=εi
# 自感与互感
# 互感
![]()
设L1 的电流为i1,在L2 中产生的磁通量为Ψ12=N2B1S
互感电动势为:
εm=−dtdΨ=−Mdtdi−idtdM
M 称为两线圈的互感系数,单位为亨利H,1H=1Wb/A
# 互感的计算
εm=−Mdtdi或{Ψ12=Mi1Ψ21=Mi2
M12=M21
# 自感
![]()
一线圈通有单位电流时,通过线圈自身的全磁通等于该线圈的自感系数。
全磁通:
Ψ=Li
自感系数L:
L=iΨ
取决于回路的大小、形状、匝数以及μ
εL∝L{L大,εL大→阻碍电路变化的阻力大L小,εL小→阻碍电路变化的阻力小
# 自感的计算
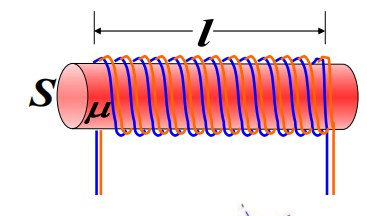
![]()
L=iΨ=μn2V
M=μn1n2V
理想耦合:两线圈紧密缠绕,彼此磁场完全穿过,无漏磁
M=L1L2
当有漏磁时:
M=kL1L2
# 应用
![]()
顺接:磁场彼此加强,自感电动势和互感电动势同向
ε=ε1+ε2+ε12+ε21=−L1dtdi−L2dtdi−Mdtdi−Mdtdi
L=L1+L2+2M
![]()
反接:磁场彼此减弱,自感电动势和互感电动势反向
∣ε∣=∣ε1+ε2∣−∣ε12+ε21∣
L=L1+L2−2M
# LR 电路
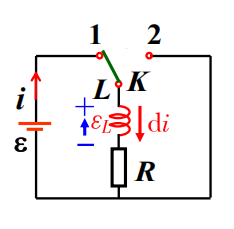
![]()
$$
\varepsilon_L-iR+\varepsilon=0
$$
ε−Ldtdi=iR
dtdi+LRi=Lε
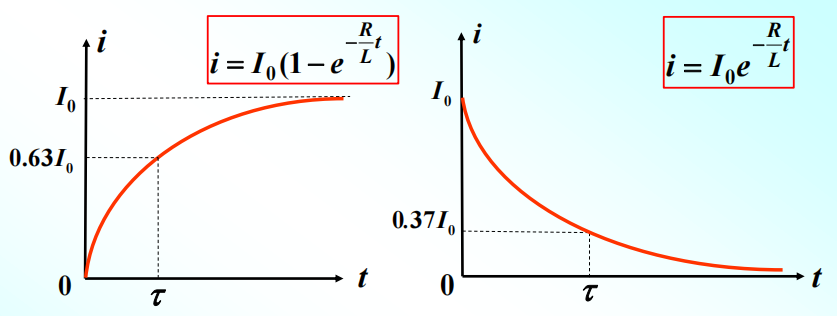
t=0时,i=0→i=Rε+Ce−Rt/L=Rε(1−e−Rt/L)
![]()
$$
\varepsilon_L-iR=0
$$
−Ldtdi=iR
t=0时,i=I→i=Rεe−Rt/L
![]()
RL 称为电路的时间常数
# 磁场的能量
# 自感储存磁能
电容器充电后就储存了电场能量:
We=21CU2
![]()
电流增加di,电源克服εL 做功为dA
Wm=A=21LI2
# 磁能与磁能密度
通有电流I 的长直螺线管储存的磁能为:
Wm=2μ0B2V
磁能密度:
wm=VWm=2μ0B2=21B⋅H
其中,H=μ0B
# 麦克斯韦方程组
静电场:静止电荷激发
∮SD静⋅dS=S内∑q0,D=εE
∮LE静⋅dl=0
稳恒磁场:恒定电流激发
∮SB⋅dS=0
∮LH⋅dl=L套连∑Ii
非稳恒磁场:变化的磁场激发
∮LEi⋅dS=0
∮C2Ei⋅dl=−∬S∂t∂B⋅dS
# 位移电流
安培环路定理:
∮LH⋅dl=∑l=∫Sj⋅dS
j 是穿过以闭合回路L 为边界的任意曲面S 上的传到电流的电流密度
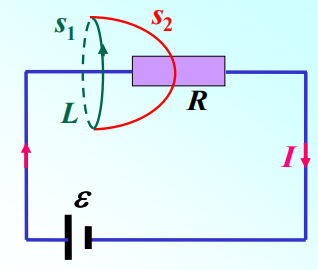
![]()
以L 为边界取两个不同的曲面s1 和s2,由于恒定情况下电流是连续的,通过这两个曲面的电流相等,即
∫S1j⋅dS=∫S2j⋅dS
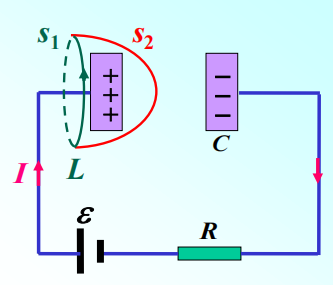
![]()
只考虑电容的左极板,取s1 和s2 组成的高斯面:
单位时间内电荷的增量=进来的电荷流量−出去的电荷流量
dtdq=−∬S1j⋅dS−∬S2j⋅dS−−①
∮SD⋅dS=∑q
dtdq=dtd∮SD⋅dS=∮S∂t∂D⋅dS−−②
由①②得:
−∮Sj⋅dS=∮S∂t∂D⋅dS
⇒∮S(j+∂t∂D)⋅dS=0
变化的电场可以等效地视为一种 “电流”,即位移电流
位移电流密度:
jD=∂t∂D=ε∂t∂E
穿过空间任意曲面的位移电流为:
ID=∬SjD⋅dS=∬S∂t∂D⋅dS=dtd∮SD⋅dS=dtdΦD
# 全电流
位移电流和传导电流的和
传导电流:
I=∬Sj⋅dS
位移电流:
ID=∬SjD⋅dS
全电流:
∮LH⋅dl=∬S(j+∂t∂D)⋅S
考虑真空
B=μ0H,D=ε0E
如果仅存在位移电流,即仅有变化的电场:
∮LB⋅dl=μ0ε0dtd∬SE⋅dS
而变化的磁场会激发电场:
∮LEi⋅dl=−∬S∂t∂B⋅dS
在导体中传导电流远大于位移电流




 $$
\varepsilon_L-iR+\varepsilon=0
$$
$$
\varepsilon_L-iR+\varepsilon=0
$$
 $$
\varepsilon_L-iR=0
$$
$$
\varepsilon_L-iR=0
$$