电磁感应

法拉第电磁感应定律

感应电动势：单位\(1V=1Wb/s\) \[ \varepsilon_i=-N\frac{d\Phi}{dt} \] 任一回路中： \[ \Phi=\iint_S\vec{B}\cdot d\vec{S}=\iint_S B\cos \theta \cdot dS \] 从\(t_1\to t_2\)时间内，通过回路导线任一截面的感应电量： \[ q=\int_{t_1}^{t_2}Idt=-\frac{N}{R}\int_{\Phi_1}^{\Phi_2}d\Phi=-\frac{N}{R}(\Phi_2-\Phi_1) \]

电源

提供非静电力，维持稳恒电流

正电荷在静电场力的作用下从A经过导线移到B，并与B上的负电荷中和，直至板间电势差消失。要维持稳恒电流，须使正电荷从B经BA内移至A上，使 两板间有恒定的电势差。

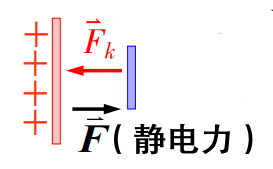
非静电场： \[ \vec{E_k}=\vec{F_k}/q \] 方向：电源内部由负极指向正极

电源电动势：单位正电荷从负极经电源内部移至正极时，非静电力做的功。 \[ \varepsilon=\frac{A}{q}=\int_{内部-}^{内部+}\vec{E_k}\cdot d\vec{l} \]

感应电动势

动生电动势

导体在磁场中运动时产生的感应电动势 \[ \varepsilon_i=vBL \]

\[ \vec{F_k}=-e\vec{v}\times \vec{B} \]

\[ \vec{E_k}=\vec{v}\times\vec{B} \]

感生电动势

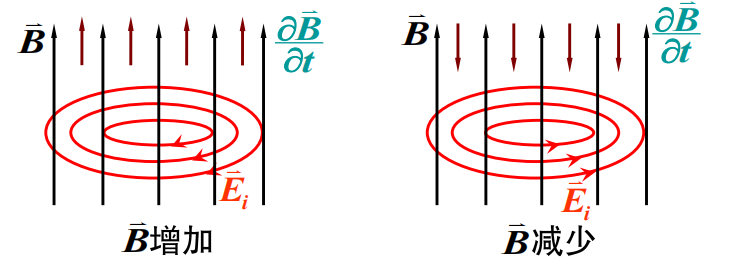
\[ \varepsilon_i=-\frac{d\Phi}{dt}=-\frac{d}{dt}\iint_{S}\vec{B}\cdot d\vec{S}=-\iint_S \frac{\partial \vec B}{\partial t}\cdot d\vec{S} \]

考虑闭合回路：

\[ \oint_L\vec{E_i}\cdot d\vec{l}=-\iint_S \frac{\partial \vec B}{\partial t}\cdot d\vec{S} \] 方向由楞次定律判断

感应电场

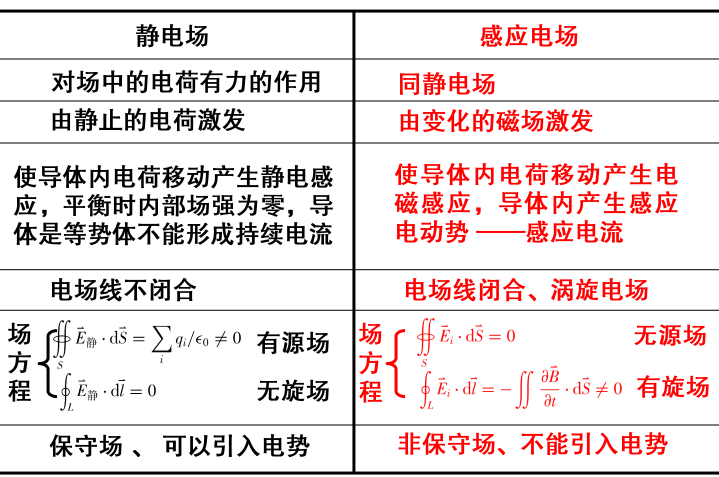
感应电场是产生感应电动势的机制，不是静电场

\(E_静\)为保守力场： \[ \oint\vec{E_静}\cdot d\vec{l}=0 \] \(\vec{E_i}\)是非保守力场： \[ \oint\vec{E_i}\cdot d\vec{l}\neq 0 \]

感应电场的计算

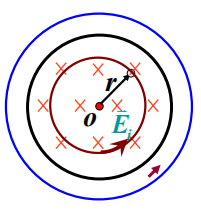\[ r<R时,E_i=-\frac{r}{2}\frac{\partial B}{\partial t} \] \[ r > R时,E_i=\frac{R^2}{2r}\frac{\partial B}{\partial t} \]

\(\vec E_i\)是涡旋场--非保守场，不能引入势函数，但是它对在场中的导体提供电动势

导体不闭合时\(\rightarrow\)使到体内电荷重新分布\(\rightarrow\)产生\(\vec{E_静}\rightarrow\)到体内总电场达到平衡\(\rightarrow\)由于电荷的存在空间出现电势\(\rightarrow \Delta U=\varepsilon_i\)

自感与互感

互感

设\(L_1\)的电流为\(i_1\)，在\(L_2\)中产生的磁通量为\(\Psi_12=N_2B_1S\)

互感电动势为： \[ \varepsilon_m=-\frac{d\Psi}{dt}=-M\frac{di}{dt}-i\frac{dM}{dt} \] \(M\)称为两线圈的互感系数，单位为亨利\(H\)，\(1H=1Wb/A\)

互感的计算

\[ \varepsilon_m =-M\frac{di}{dt}或\left\{\begin{matrix} \Psi_{12}=Mi_1 \\ \Psi_{21}=Mi_2 \end{matrix}\right. \]

\[ M_{12}=M_{21} \]

自感

一线圈通有单位电流时,通过线圈自身的全磁通等于该线圈的自感系数。

全磁通： \[ \Psi = Li \] 自感系数\(L\)： \[ L=\frac{\Psi}{i} \] 取决于回路的大小、形状、匝数以及\(\mu\) \[ \varepsilon_L\propto L\left\{\begin{matrix} L大，\varepsilon_L大\rightarrow 阻碍电路变化的阻力大 \\ L小，\varepsilon_L小\rightarrow 阻碍电路变化的阻力小 \end{matrix}\right. \]

自感的计算

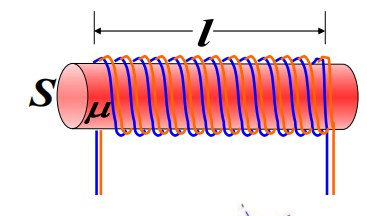\[ L=\frac{\Psi}{i}=\mu n^2 V \]

\[ M=\mu n_1n_2 V \]

理想耦合：两线圈紧密缠绕，彼此磁场完全穿过，无漏磁 \[ M=\sqrt{L_1L_2} \] 当有漏磁时： \[ M=k\sqrt{L_1L_2} \]

应用

顺接：磁场彼此加强，自感电动势和互感电动势同向 \[ \varepsilon=\varepsilon_1+\varepsilon_2+\varepsilon_{12}+\varepsilon_{21} =-L_1\frac{di}{dt}-L_2\frac{di}{dt}-M\frac{di}{dt}-M\frac{di}{dt} \]

\[ L=L_1+L_2+2M \]

反接：磁场彼此减弱，自感电动势和互感电动势反向 \[ |\varepsilon|=|\varepsilon_1+\varepsilon_2|-|\varepsilon{12}+\varepsilon{21}| \]

\[ L=L_1+L_2-2M \]

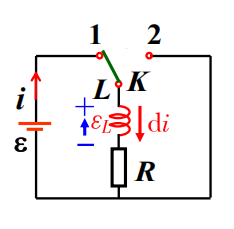
LR电路

\[ \varepsilon_L-iR+\varepsilon=0 \]

\[ \varepsilon-L\frac{di}{dt}=iR \]

\[ \frac{di}{dt}+\frac{R}{L}i=\frac{\varepsilon}{L} \]

\[ t=0时,i=0\rightarrow i=\frac{\varepsilon}{R}+Ce^{-Rt/L}=\frac{\varepsilon}{R}(1-e^{-Rt/L}) \]

\[ \varepsilon_L-iR=0 \]

\[ -L\frac{di}{dt}=iR \]

\[ t=0时,i=I\rightarrow i=\frac{\varepsilon}{R}e^{-Rt/L} \]

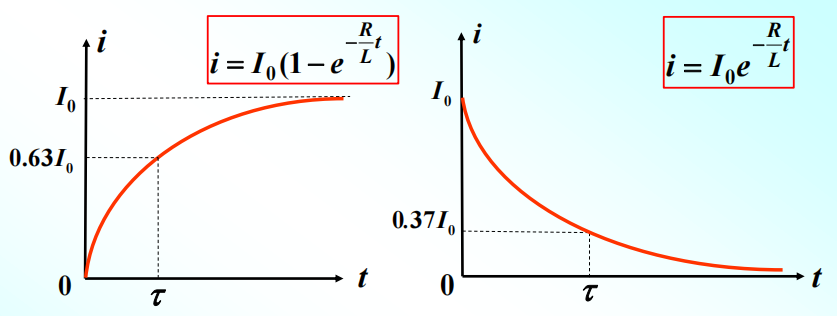
\(\frac{L}{R}\)称为电路的时间常数

磁场的能量

自感储存磁能

电容器充电后就储存了电场能量： \[ W_e=\frac{1}{2}CU^2 \]

电流增加\(di\)，电源克服\(\varepsilon_L\)做功为\(dA\) \[ W_m=A=\frac{1}{2}LI^2 \]

磁能与磁能密度

通有电流\(I\)的长直螺线管储存的磁能为： \[ W_m=\frac{B^2}{2\mu_0}V \] 磁能密度： \[ w_m=\frac{W_m}{V}=\frac{B^2}{2\mu_0}=\frac{1}{2}\vec{B}\cdot\vec{H} \]

\[ 其中,\vec{H}=\frac{\vec B}{\mu_0} \]

麦克斯韦方程组

静电场：静止电荷激发 \[ \oint_S\vec{D_静}\cdot d\vec{S}=\sum_{S_内}q_0,\vec{D}=\varepsilon\vec{E} \]

\[ \oint_{L}\vec{E_静}\cdot d\vec{l}=0 \]

稳恒磁场：恒定电流激发 \[ \oint_S\vec{B}\cdot d\vec{S}=0 \]

\[ \oint_L\vec{H}\cdot d\vec{l}=\sum_{L套连}I_i \]

非稳恒磁场：变化的磁场激发 \[ \oint_{L}\vec{E_i}\cdot d\vec{S}=0 \]

\[ \oint_{C_2}\vec{E_i}\cdot d\vec{l}=-\iint_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S} \]

位移电流

安培环路定理： \[ \oint_L\vec{H}\cdot d\vec{l}=\sum l=\int_S\vec{j}\cdot d\vec{S} \] \(\vec{j}\)是穿过以闭合回路\(L\)为边界的任意曲面\(S\)上的传到电流的电流密度

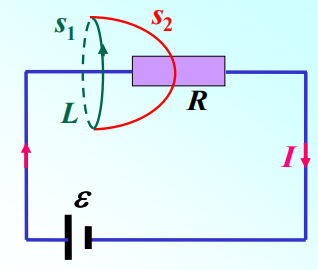
以\(L\)为边界取两个不同的曲面\(s_1\)和\(s_2\)，由于恒定情况下电流是连续的，通过这两个曲面的电流相等，即 \[ \int_{S_1}\vec{j}\cdot d\vec{S}=\int_{S_2}\vec{j}\cdot d\vec{S} \]

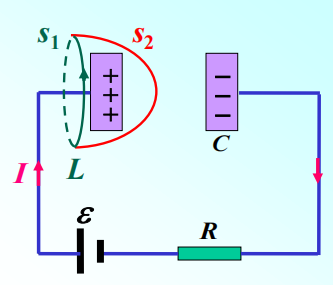
只考虑电容的左极板，取\(s_1\)和\(s_2\)组成的高斯面： \[ 单位时间内电荷的增量 = 进来的电荷流量-出去的电荷流量 \]

\[ \frac{dq}{dt}=-\iint_{S_1}\vec{j}\cdot d\vec{S}-\iint_{S_2}\vec{j}\cdot d\vec{S}--① \]

\[ \oint_{S}\vec{D}\cdot d\vec{S}=\sum q \]

\[ \frac{d}{dt}q=\frac{d}{dt}\oint_{S}\vec{D}\cdot d\vec{S}=\oint_S\frac{\partial \vec{D}}{\partial t}\cdot d\vec{S}--② \]

由①②得： \[ -\oint_S\vec{j}\cdot d\vec{S}=\oint_S\frac{\partial{\vec D}}{\partial t}\cdot d\vec{S} \]

\[ \Rightarrow \oint_S(\vec{j}+\frac{\partial{\vec D}}{\partial t})\cdot d\vec{S}=0 \]

变化的电场可以等效地视为一种“电流”，即位移电流

位移电流密度： \[ \vec{j_D}=\frac{\partial \vec D}{\partial t}=\varepsilon\frac{\partial \vec E}{\partial t} \] 穿过空间任意曲面的位移电流为： \[ I_D=\iint_S\vec{j_D}\cdot d\vec S=\iint_S\frac{\partial \vec D}{\partial t}\cdot d\vec{S}=\frac{d}{dt}\oint_{S}\vec{D}\cdot d\vec{S}=\frac{d}{dt}\Phi_D \]

全电流

位移电流和传导电流的和

传导电流： \[ I=\iint_S\vec{j}\cdot d\vec S \] 位移电流： \[ I_D=\iint_S\vec{j_D}\cdot d\vec{S} \] 全电流： \[ \oint_L\vec{H}\cdot d\vec{l}=\iint_S(\vec{j}+\frac{\partial{\vec D}}{\partial t})\cdot \vec{S} \] 考虑真空 \[ \vec{B}=\mu_0\vec{H},\vec{D}=\varepsilon_0\vec E \] 如果仅存在位移电流，即仅有变化的电场： \[ \oint_L\vec B\cdot d\vec l=\mu_0\varepsilon_0\frac{d}{dt}\iint_S\vec E\cdot d\vec S \] 而变化的磁场会激发电场： \[ \oint_{L}\vec{E_i}\cdot d\vec{l}=-\iint_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S} \] 在导体中传导电流远大于位移电流