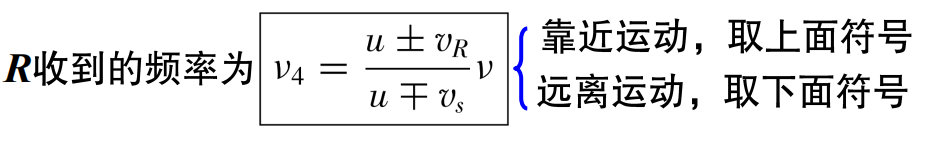# 简谐振动

# 方程表示

Q 做简谐运动：

$$F_{合}=-kx_i,w=\sqrt{\frac{k}{m}}$$

$$\frac{d^2x}{dt^2}+w^2x=0$$

方程的解：

$$x=A\cos(wt+\varphi)$$

$$A=\sqrt{x_0^2+\frac{v_0^2}{w^2}}$$

$$\tan\varphi=-\frac{v_0}{x_0w}$$

# 矢量旋转表示

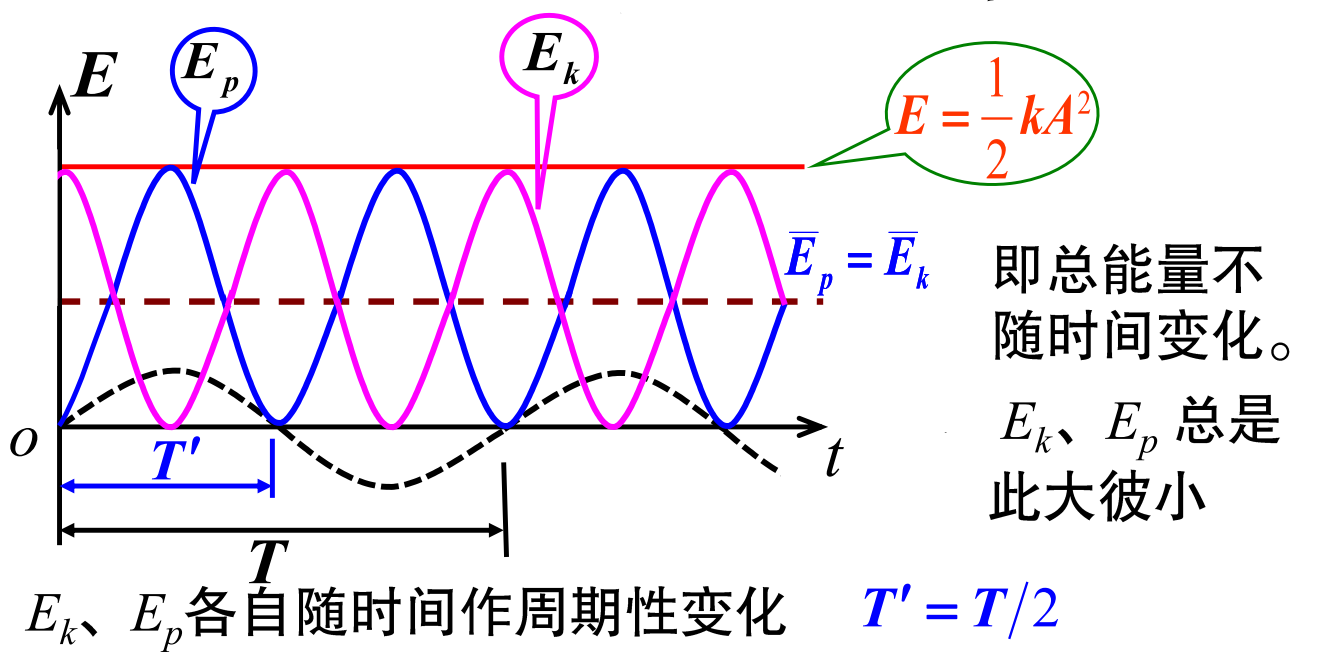
# 简谐振动的能量

动能：

$$E_k=\frac{1}{2}mv^2=\frac{1}{2}kA^2\sin^2(wt+\varphi)$$

势能：

$$E_p=\frac{1}{2}kx^2=\frac{1}{2}kA^2\cos^2(wt+\varphi)$$

总能量：

$$E=E_k+E_p=\frac{1}{2}kA^2$$

动能和势能的时间平均值：

$$\bar{E_k}=\frac{1}{T}\int_0^T\frac{1}{2}kA^2\sin^2(wt+\varphi)dt=\frac{1}{4}kA^2$$

$$\bar{E_p}=\frac{1}{T}\int_0^T\frac{1}{2}kA^2\cos^2(wt+\varphi)dt=\frac{1}{4}kA^2$$

能量 - 时间曲线

能量 - 位移曲线

$$x=A\cos(wt+\varphi)$$

$$E_k=\frac{1}{2}kA^2\sin^2(wt+\varphi)\Rightarrow E_k=\frac{1}{2}k(A^2-x^2)$$

$$E_p=\frac{1}{2}kA^2\cos^2(wt+\varphi)\Rightarrow E_p=\frac{1}{2}kx^2$$

# 振动的合成和分解

$$A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos(\varphi_2-\varphi_1)}$$

$$\tan\varphi=\frac{A_1\sin\varphi_1+A_2\sin\varphi_2}{A_1\cos\varphi_1+A_2\cos\varphi_2}$$

# 同方向 N 个同频率简谐振动的合成

# 同方向不同频率简谐振动的合成

不是简谐振动，但是振动

振幅时大时小：拍

角频率 w：

$$w=\frac{w_2-w_1}{2}$$

周期$\tau$：

$$\tau=\frac{2\pi}{w_2-w_1}$$

频率$\nu$

$$\nu=\frac{1}{\tau}=\frac{w_2-w_1}{2\pi}=\nu_2-\nu_1$$

拍在两分振动的频率相差不大时更为明显

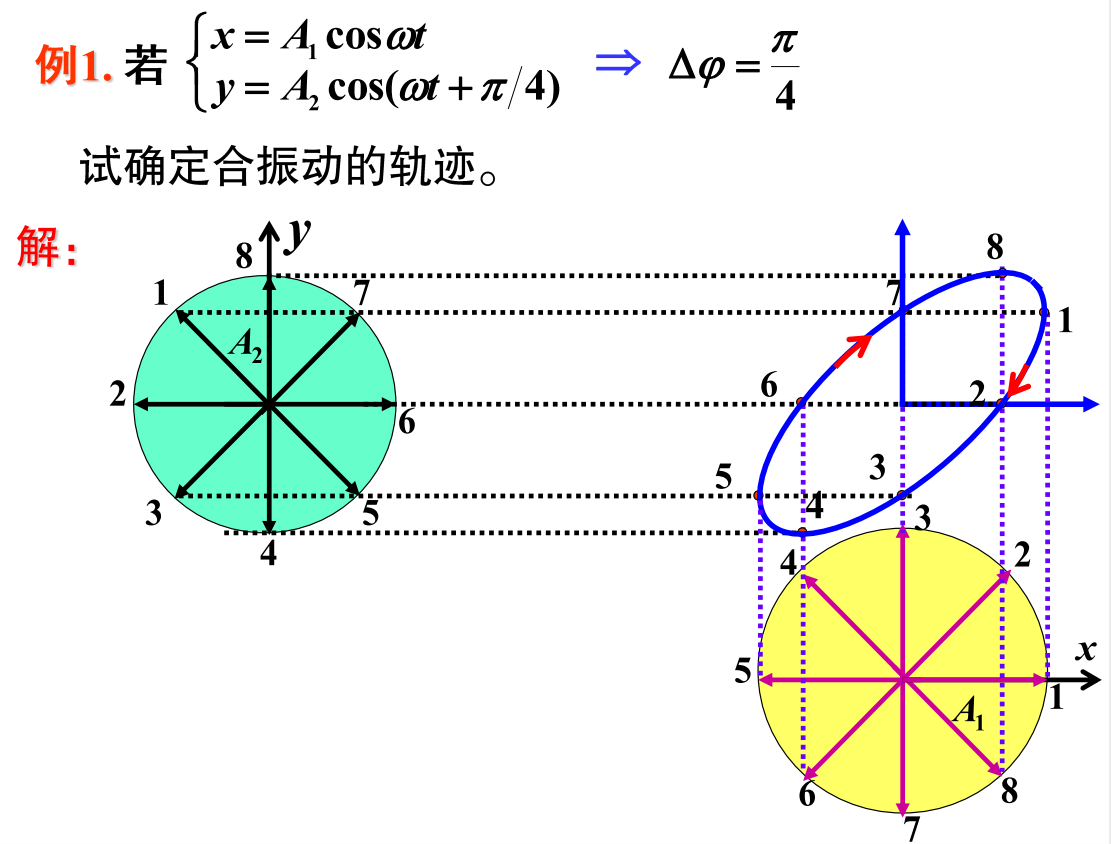
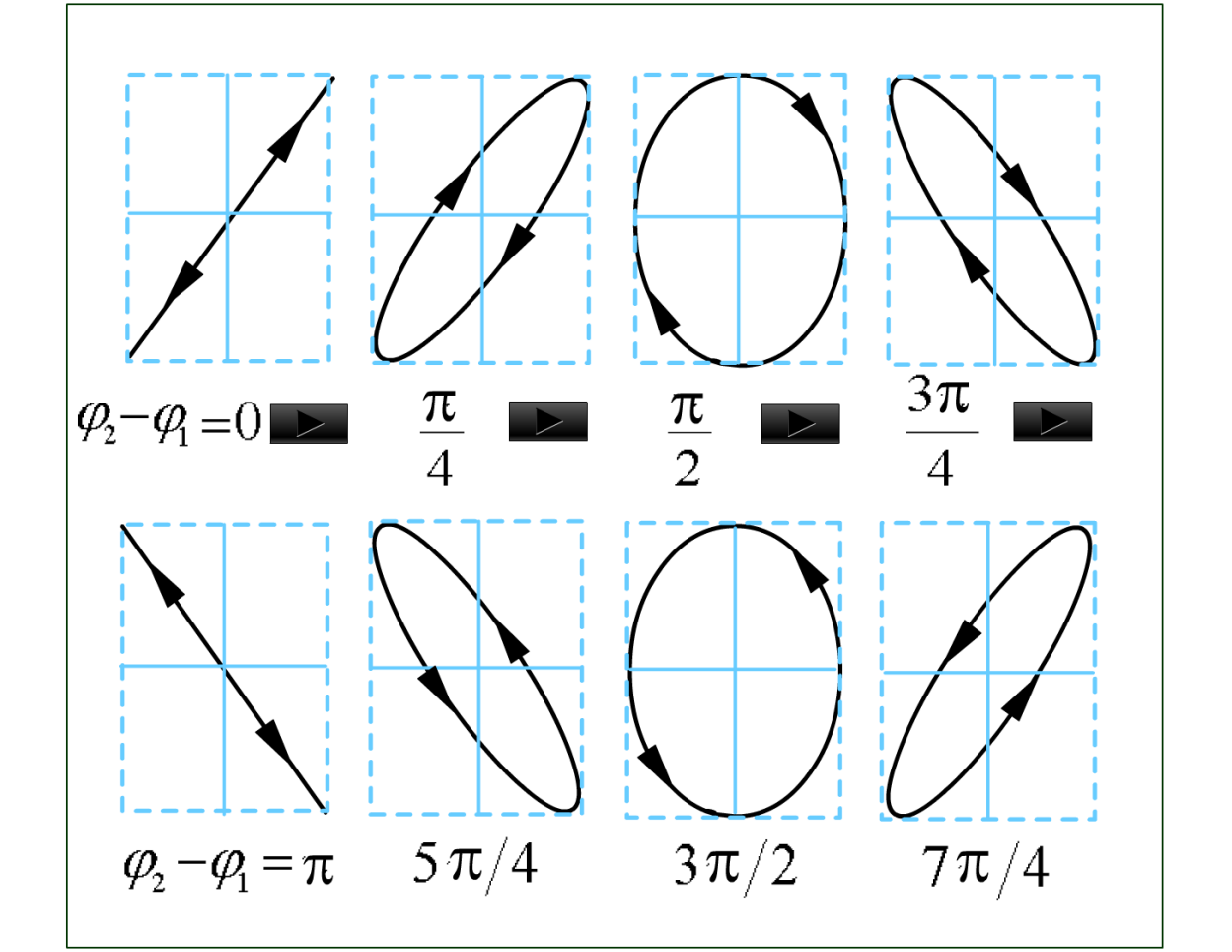
# 相互垂直同频率简谐振动的合成

$x=A_1\cos(wt+\varphi_1),y=A_2\cos(wt+\varphi_2)$：

$$\large\frac{x^2}{A_1^2}+\frac{y^2}{A_2^2}-\frac{2xy}{A_1A_2}\cos\Delta\varphi=\sin^2\Delta\varphi$$

一般情况下，质点的轨迹是椭圆

• $\Delta\varphi\in(0,\pi)$，质点沿顺时针方向运动，右旋
• $\Delta\varphi\in(-\pi,0)$，质点沿逆时针方向运动，左旋

讨论$\Delta \varphi$

当$(\varphi_2-\varphi_1)=0/\pi$ 时，为直线

当$(\varphi_2-\varphi_1)=\frac{1}{2}\pi/-\frac{1}{2}\pi$ 时，为正椭圆

• 当$A_1=A_2$ 时，正椭圆为圆

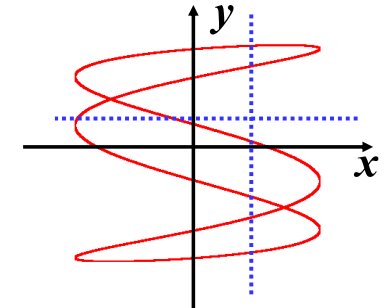
# 相互垂直不同频率的简谐运动的合成

两分振幅频率相差很小

可近似看做两个频率相同，而$\varphi_2-\varphi_1$ 随 t 不断变化

$\Delta\varphi$ 从

$$0\to\frac{1}{2}\pi\to\pi\to\frac{3}{2}\pi\to2\pi$$

合运动轨迹$(0\sim \pi的情况)$ 从

直线->斜椭圆->正椭圆->斜椭圆->直线

两振动的频率成整数比

$$\frac{w_1}{w_2}=\frac{n}{m}$$

合成轨迹为稳定的闭合曲线–李萨如图形

可以测量信号频率

$$\frac{w_x}{w_y}=\frac{\nu_x}{\nu_y}=\frac{x出现的次数}{y出现的次数}$$

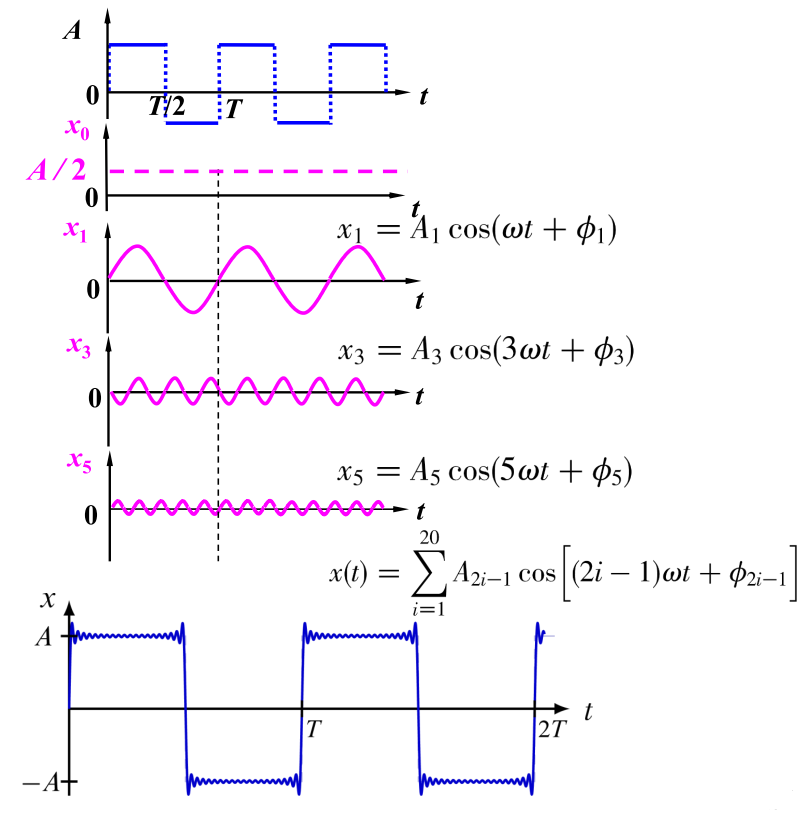
# 谐振分析

# 阻尼与受迫振动 & 共振

# 阻尼

# 动力学方程

$$\frac{d^2x}{dt^2}+2\beta\frac{dx}{dt}+w_0^2x=0$$

$$w_0^2=\frac{k}{m},2\beta=\frac{\gamma}{m}$$

# 运动学特征

弱阻尼$\beta<w_0$

$$ x=A_0e^{-\beta t}\cos(wt+\varphi_0) $$

$$w=\sqrt{w_0^2-\beta^2}$$

• 振幅随 t 按指数衰减

• 是准周期运动，出现两次极大的时间间隔

  $$T=\frac{2\pi}{w}=\frac{2\pi}{\sqrt{w_0^2-\beta^2}}>\frac{2\pi}{w_0}=T_0$$

  周期变长，振动变慢

• 能量 E 随振幅 A 的减小而衰减$E\propto A^2$

过阻尼$\beta>w_0$

• 非周期性运动
• 无振动发生

临界阻尼$\beta=w_0$

振子刚好处于一个从准周期振动转变到非周期运动的临界状态

# 受迫振动

设强迫力为$F(t)=F_m\cos wt$

# 动力学方程

$$\frac{d^2x}{dt^2}+2\beta\frac{dx}{dt}+w_0^2x=h\cos wt$$

$$w_0^2=\frac{k}{m},2\beta=\frac{\gamma}{m},h=\frac{F_m}{m}$$

稳态时的受迫振动按简谐运动的规律变化，频率为$w$

将稳态方程带入解得：

$$振幅：A=\frac{h}{\sqrt{(w_0^2-w^2)^2+4\beta^2w^2}}$$

$$相位：\tan\varphi=-\frac{2\beta w}{w_0^2-w^2}$$

# 稳定受迫振动和简谐振动的区别

1. 受力不同

2. 弹黄振子：

   • $w_0$ 是系统固有的
   • $A,\psi$ 取决于初始条件

   受迫振动：

   • $w_0$ 受外力影响
   • $A,\psi$ 受外力和系统共同决定

3. 简谐振动能量守恒

# 共振

$\frac{dA}{dw}=0$

共振频率为：

$$w_r=w=\sqrt{w_0^2-2\beta^2}$$

共振振幅为：

$$A_r=\frac{h}{2\beta\sqrt{w_0^2-\beta^2}}$$

若$\beta \ll w_0$，则$w_r\approx w_0,A_r=\frac{h}{2\beta}$，称为尖锐共振

当$\beta\to 0$，即弱阻尼时，共振发生在固有频率处，称为尖锐共振

# 机械波

# 产生条件

1. 波源
2. 弹性介质：无穷多质点通过相互之间的弹性力作用组合在一起的连续介质。可以是固体、液体和气体。波源处质点的振动通过弹性介质中的弹性力，将振动状态在介质中由近及远地传播开去，从而形成机械波。

# 波的分类

横波：振动方向和传播方向垂直，如绳波，电磁波

• 有波峰，波谷，只存在于固体中

纵波：振动方向和传播方向相同，如声波

• 有疏密之分，存在于固液气中

# 波的描述

波的$T$ 和$\nu$ 取决于波源

波速$u$ 取决于介质（取决于介质的弹性模量和密度）

波长$\lambda$ 由波源和传输介质共同决定

# 平面简谐波

波源简谐振动，波面为平面

# 波函数

波源在 o 点，以速度 u 向 x 轴方向传播

在 p 点，振动时间比 o 点晚$\frac{x}{u}$，相位比 o 点落后w\frac{x}

p 点 t 时刻振动位移为

$$y=A\cos(wt-w\frac{x}{u})$$

# 波函数的意义

1. x 一定时，$x=x_1$ 为$x_1$ 处质点的振动方程

2. t 一定时，$t=t_1$ 为$t_1$ 时刻波形方程

3. 当$x,t$ 都不固定时，波函数描述了波形的传播

   考察$t_1$ 和$t_2=t_1+\Delta t$ 时刻波形方程

   $$y_1=A\cos w(t_1-\frac{x}{u})$$

   $$y_2=A\cos w(t_2-\frac{x'}{u})=A\cos w(t1 + \Delta t-\frac{x'}{u})=A\cos (wt_1 - \frac{w(x'-u\Delta t)}{u})$$

   当$x'=x + u\Delta t$ 时，$y_1=y_2$，说明经过$\Delta t$ 时间，整个波形向前平移了一段距离$\Delta x=u\Delta t$

# 一般形式

波源 o 初相位$\psi\neq 0$，波源振动方程为$y=\cos(wt+\varphi)$

则 p 点振动方程为：

P 点落后 O 点的相位：$w\Delta t=wx/u$

$$y=\cos(wt+(\varphi-wx/u))$$

P 点落后 O 点的振动时间：$\Delta t=x/u$

$$y=\cos(w(t - x/u)+\varphi)$$

根据$w=\frac{2\pi}{T}=2\pi\nu,u=\frac{\lambda}{T}=\lambda\nu$

$$y=A\cos(wt-\frac{2\pi x}{\lambda}+\varphi)$$

$$y=A\cos[2\pi(\frac{t}{T}-\frac{x}{\lambda})+\varphi]$$

定义波数k=\frac{2\pi}

$$y(x,t)=A\cos((wt-kx)+\varphi)=Ae^{i(wt-kx)+i\varphi}$$

相位差：

$$\Delta \varphi=k\Delta x$$

# 波反向传播

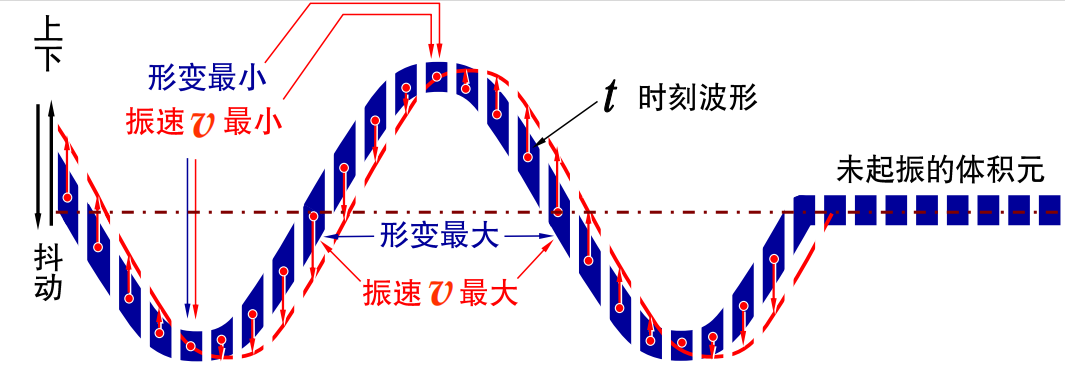
# 波的能量

# 波的能量的传播

在$x$ 处取长度为$\Delta x$，体积为$\Delta V=S\Delta x$，质量为$\Delta m=\rho\Delta V$

振动动能

$$E_k=\frac{1}{2}\rho\Delta VA^2w^2\sin^2w(t-\frac{x}{u})$$

振动势能

$$E_p=\frac{1}{2}\rho\Delta VA^2w^2\sin^2w(t-\frac{x}{u})$$

t 时刻质元的总能量

$$E=\rho\Delta VA^2w^2\sin^2w(t-\frac{x}{u})$$

体积元中动能和势能同相地随时间变化，在任一时刻都具有相同的数值

# 能量密度

能量密度：

$$w=\frac{\Delta W}{\Delta V}=\rho A^2w^2\sin^2w(t-\frac{x}{u})$$

周期

$$T'=\frac{1}{2}T$$

平均能量密度：

$$\bar{w}=\frac{1}{2}\rho A^2w^2$$

平面简谐波在各处的平均能量密度都相等

介质并不积累能量，能量随着波动的行进，从介质的这一部分传到另一部分。波动是能量传播的一种形式；波动的能量沿波速方向传播

# 能流密度

能流 P：单位时间内垂直通过某一截面的能量

$\Delta t$ 时间内通过垂直于波速截面$\Delta S$ 的能量，$\Delta W=u\Delta t\Delta Sw$，$w$ 是截面所在的能量密度

$$P=\frac{\Delta W}{\Delta t}=u\Delta S w=u\Delta S\rho A^2w^2\sin^2w(t-\frac{x}{u})$$

平均能流：在一个周期内能流的平均值

$$\bar{P}=u\Delta S \bar w=\frac{1}{2}\rho A^2w^2u\Delta S$$

能流密度$i$ 是单位时间内通过垂直于波速方向的单位面积的能量。

$$i=wu$$

平均能流密度：通过垂直于波动传播方向的单位面积的平均能流，又称为波的强度，单位$W/m^2$

$$I=\frac{\bar P}{\Delta S}=u\bar w=\frac{1}{2}\rho A^2w^2u$$

矢量表示，方向和 u 相同

$$\vec{I}=\frac{1}{2}\rho A^2w^2\vec u$$

穿过各波面的平均能流应相等

$$ \frac{\bar P_1}{\bar P_2}=1=\frac{A_1^2}{A_2^2}\frac{S_1}{S_2}\\ A_1=A_2 $$ $$ \frac{\bar P_1}{\bar P_2}=1=\frac{A_1^2}{A_2^2}\frac{S_1}{S_2}=\frac{A_1\cdot4\pi r_1}{A_2\cdot4\pi r_2}=1\\ A_1\neq A_2 $$ 如果距波源单位距离的振幅为A，则距波源r处的振幅为$A/r$

# 衍射 & 干涉

# 干涉

相干条件：

1. 频率相同
2. 振动方向相同
3. 相位差恒定

两波源$S_1,S_2$ 振动表达式为：

$$y_{10}=A_1\cos(wt+\varphi_{10})$$

$$y_{20}=A_2\cos(wt+\varphi_{20})$$

传播到 p 点引起的振动为：

$$y_{1}=A_1\cos(wt+\varphi_{10}-\frac{2\pi}{\lambda}r_1)$$

$$y_{2}=A_2\cos(wt+\varphi_{20}-\frac{2\pi}{\lambda}r_2)$$

两分振动相位差为：

$$\Delta \varphi=(\varphi_{20}-\varphi_{10})-\frac{2\pi}{\lambda}(r_2-r_1)$$

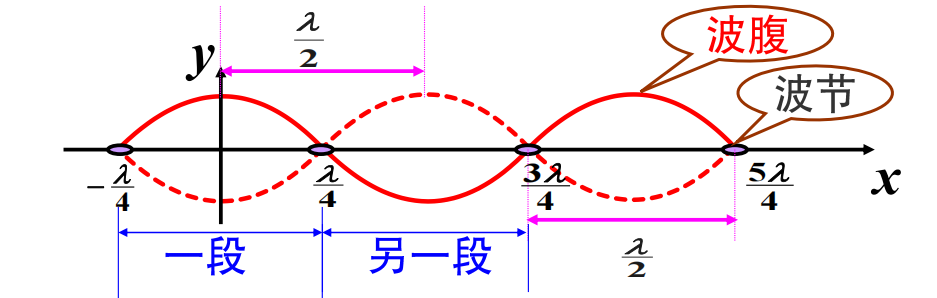
# 驻波

振幅、频率、传播速度都相同的两列相干波，在同一直线上沿相反方向传播时叠加而形成的一种特殊的干涉现象。

设有两列相干波，分别沿 x 轴正、负方向传播，选初相位均为零的表达式为：

$$y_1=A\cos(wt-\frac{2\pi}{\lambda}x),y_2=A\cos(wt+\frac{2\pi}{\lambda}x)$$

$$y=y_1+y_2=2A\cos\frac{2\pi}{\lambda}x\cdot\cos wt$$

特点：

• 振幅呈周期性分布：

  $$|2A\cos\frac{2\pi}{\lambda}x|$$

  振幅最大的称为波腹：

  $$x=k\frac{\lambda}{2}$$

  振幅最小的称为波节：

  $$x=(2k+1)\frac{\lambda}{4}$$

• 两个波节之间一段中的各点振动位相相同，在波节两侧的点 (邻近两段) 振动位相相反

• 驻波不传播能量

  • 驻波的动能主要集中在波腹，势能主要集中在波节。能量在相邻的波腹和波节间往复变化
  • 驻波中没有振动状态或位相的传播，也没有能量的传播，实际上是分段振动
  • 驻波不是波动，而是一种特殊形式的振动

# 弦线上的驻波

一弦线两段固定，两端点为波节

可能驻波长：

$$L=n\frac{\lambda}{2},n=1,2,3,...$$

# 半波损失

$\rho u$ 大的是波密，$\rho u$ 小的是波疏

从光疏射向光密的反射光有半波损失

# 多普勒效应

波源和接收器都静止$v_s=0,v_R=0$

$$v1=v$$

波源静止，接收器运动$v_s=0,v_R\neq 0$

$$靠近：v_2=\frac{u+v_R}{u}v$$

$$远离：v_2=\frac{u-v_R}{u}v$$

波源运动，接收器静止$v_s\neq 0,v_R=0$

$$靠近：v_3=\frac{u}{u-v_s}v$$

$$远离：v_3=\frac{u}{u+v_s}v$$

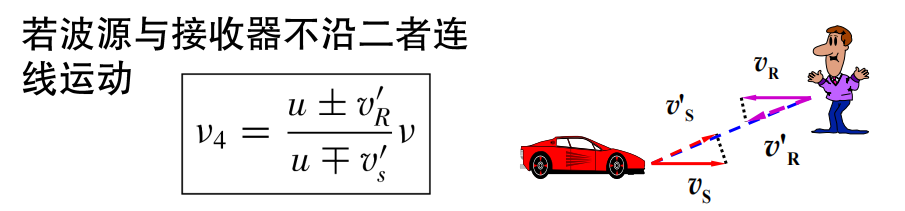
两个都运动：

# 冲击波和马赫锥

若波源速度超过波速，$v_s\gg u$，各时刻波源发出波的波前的包络面为一个以波源为顶点的圆锥面

马赫锥的半顶角：

$$\sin\alpha=\frac{u}{v_s}=\frac{1}{M}$$

当$u=v_s$ 时，马赫锥的半顶角为\frac{\pi}

# 电磁震荡和电磁波

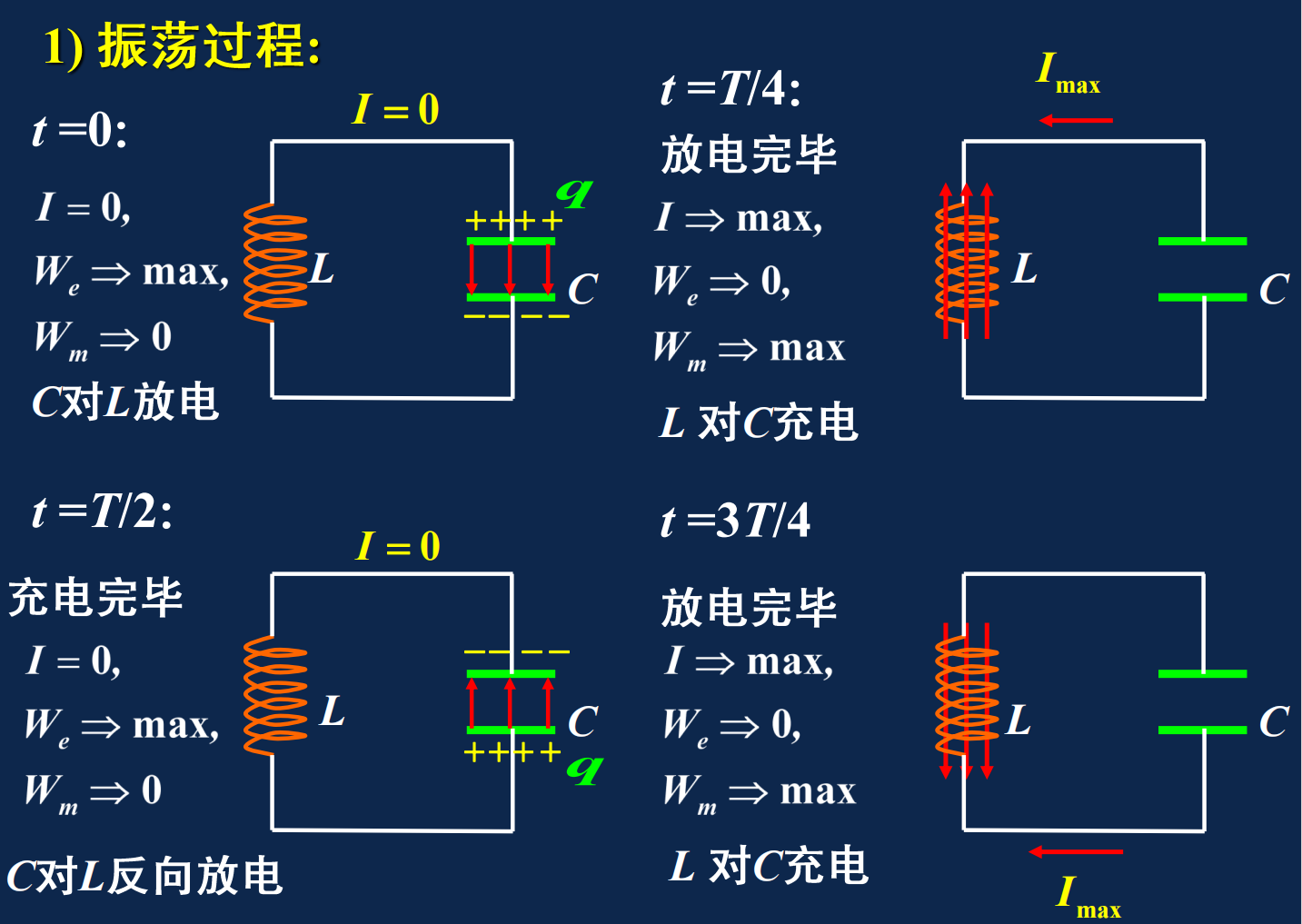
# 电磁震荡

LC 电路，无阻尼振荡：电路中电量和电流的周期性变化

产生的电磁振荡是无阻尼自由振荡

# 与简谐振动对比

电量随时间变化：

$$q=Q_0\cos(wt+\varphi)$$

电流随时间变化：

$$i=-wQ_0\sin(wt+\varphi)=I_0\cos(wt+\varphi+\frac{\pi}{2})$$

LC 振荡频率：

$$w=\sqrt{\frac{1}{LC}}$$

$$C=\frac{\varepsilon S}{d},L\propto N^2$$

# 电磁波的发射和传播

变化的磁场和变化的电场互相激发形成电磁波

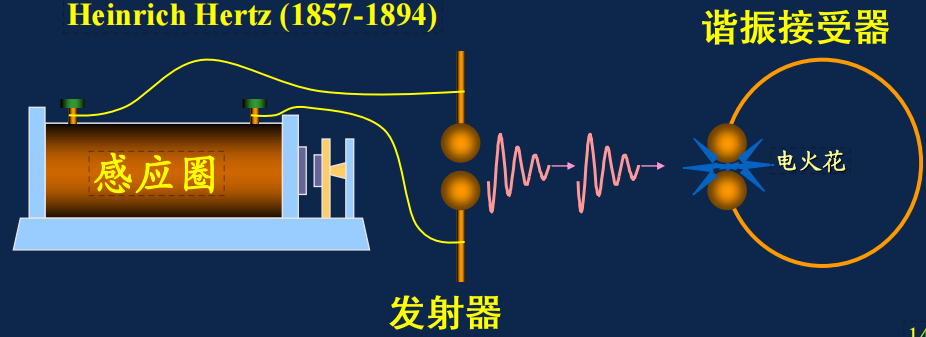
# 赫兹实验

假设两根导体棒水平，在导体棒接上高压电之后：

产生的电场和磁场相互垂直，电场水平，磁场垂直

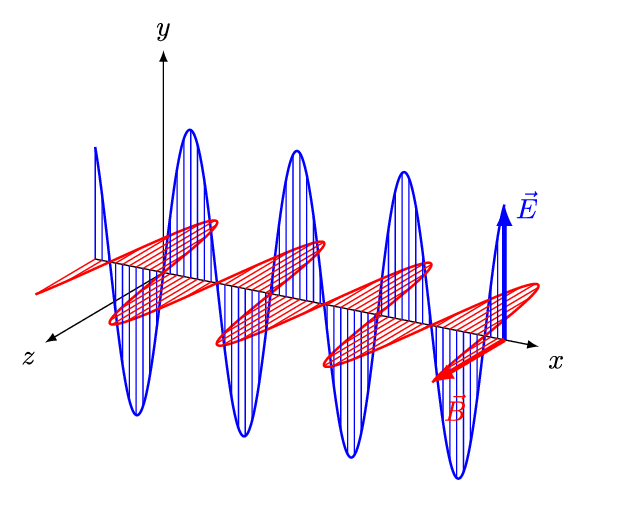
# 平面电磁波

理论和实践都证明：若$E$ 在$y$ 方向振动，则$B$ 在$z$ 方向振动，电磁波沿$x$ 方向传播。（满足右手螺旋）

波动方程：

$$\frac{\partial ^2 E}{\partial t^2}=\frac{1}{\varepsilon \mu}\frac{\partial ^2 E}{\partial x^2}$$

$$\frac{\partial ^2 H}{\partial t^2}=\frac{1}{\varepsilon \mu}\frac{\partial ^2 H}{\partial x^2}$$

电磁波波速为：

$$u=\frac{1}{\sqrt {\varepsilon \mu}}$$

当电磁波波动方程中沿$x$ 轴正向传播的平面余弦波特解为：

$$E_y=E_{y0}\cos[w(t-\frac{x}{u})+\varphi]$$

相应地磁场部分为：

$$H_z=H_{z0}\cos[w(t-\frac{x}{u})+\varphi]$$

$H$ 的振幅：

$$H_{z0}=\frac{E_{y0}}{\mu u}=\sqrt{\frac{\varepsilon}{\mu}}E_0或\sqrt{\varepsilon}E_{y0}=\sqrt{\mu}H_{z0}$$

# 电磁波的能量

电场能量密度：

$$w_e=\frac{1}{2}\varepsilon E^2$$

磁场能量密度：

$$w_m=\frac{1}{2}\mu H^2=\frac{1}{2}\varepsilon E^2$$

总能量密度：

$$w=w_e+w_m=\frac{1}{2}(\varepsilon E^2+\mu H^2)=\varepsilon E^2=\mu H^2=\sqrt{\varepsilon \mu}EH=\frac{1}{u}EH$$

能流密度：单位时间内垂直通过单位面积的电磁能量

$$S=wu=EH$$

能流密度矢量（坡印亭矢量）：

$$\vec{S}=\vec{E}\times \vec{H}$$

平均能流密度（电磁波强度）：

$$I=\bar{S}=\frac{1}{2}E_0H_0$$

因为$\sqrt{\varepsilon}E_{y0}=\sqrt{\mu}H_{z0}$ 和 $c=\frac{1}{\sqrt{\varepsilon_0\mu_0}}$

$$\bar{S}=\frac{1}{2}\varepsilon_0cE_0^2=\frac{1}{2}\mu_0cH_0^2$$