振动与波动
简谐振动
方程表示
Q做简谐运动: \[ F_{合}=-kx_i,w=\sqrt{\frac{k}{m}} \] \[ \frac{d^2x}{dt^2}+w^2x=0 \]
方程的解: \[ x=A\cos(wt+\varphi) \]
\[ A=\sqrt{x_0^2+\frac{v_0^2}{w^2}} \]
\[ \tan\varphi=-\frac{v_0}{x_0w} \]
矢量旋转表示
简谐振动的能量
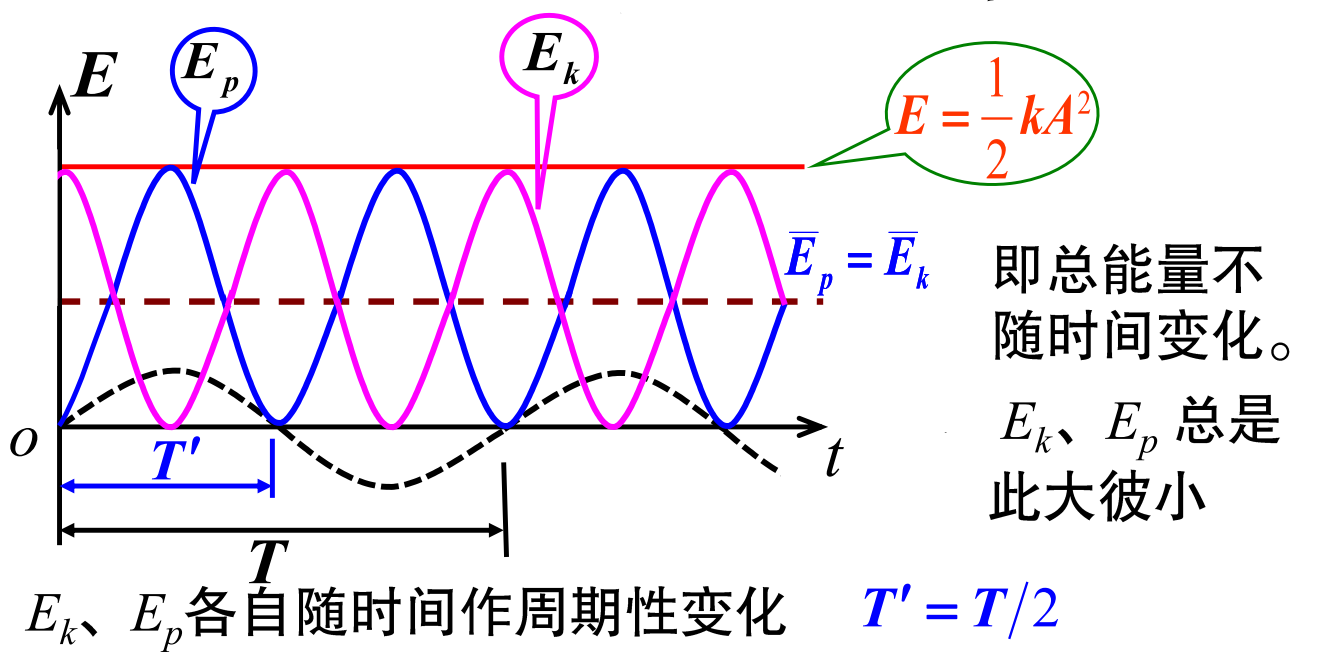
动能: \[ E_k=\frac{1}{2}mv^2=\frac{1}{2}kA^2\sin^2(wt+\varphi) \] 势能: \[ E_p=\frac{1}{2}kx^2=\frac{1}{2}kA^2\cos^2(wt+\varphi) \] 总能量: \[ E=E_k+E_p=\frac{1}{2}kA^2 \] 动能和势能的时间平均值: \[ \bar{E_k}=\frac{1}{T}\int_0^T\frac{1}{2}kA^2\sin^2(wt+\varphi)dt=\frac{1}{4}kA^2 \]
\[ \bar{E_p}=\frac{1}{T}\int_0^T\frac{1}{2}kA^2\cos^2(wt+\varphi)dt=\frac{1}{4}kA^2 \]
能量-时间曲线
能量-位移曲线 \[ x=A\cos(wt+\varphi) \] \[ E_k=\frac{1}{2}kA^2\sin^2(wt+\varphi)\Rightarrow E_k=\frac{1}{2}k(A^2-x^2) \]
\[ E_p=\frac{1}{2}kA^2\cos^2(wt+\varphi)\Rightarrow E_p=\frac{1}{2}kx^2 \]
振动的合成和分解
\[ A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos(\varphi_2-\varphi_1)} \]
\[ \tan\varphi=\frac{A_1\sin\varphi_1+A_2\sin\varphi_2}{A_1\cos\varphi_1+A_2\cos\varphi_2} \]
同方向N个同频率简谐振动的合成
同方向不同频率简谐振动的合成
不是简谐振动,但是振动
振幅时大时小:拍
角频率w: \[ w=\frac{w_2-w_1}{2} \] 周期\(\tau\): \[ \tau=\frac{2\pi}{w_2-w_1} \] 频率\(\nu\) \[ \nu=\frac{1}{\tau}=\frac{w_2-w_1}{2\pi}=\nu_2-\nu_1 \] 拍在两分振动的频率相差不大时更为明显
相互垂直同频率简谐振动的合成
\(x=A_1\cos(wt+\varphi_1),y=A_2\cos(wt+\varphi_2)\): \[ \large\frac{x^2}{A_1^2}+\frac{y^2}{A_2^2}-\frac{2xy}{A_1A_2}\cos\Delta\varphi=\sin^2\Delta\varphi \] 一般情况下,质点的轨迹是椭圆
- \(\Delta\varphi\in(0,\pi)\),质点沿顺时针方向运动,右旋
- \(\Delta\varphi\in(-\pi,0)\),质点沿逆时针方向运动,左旋
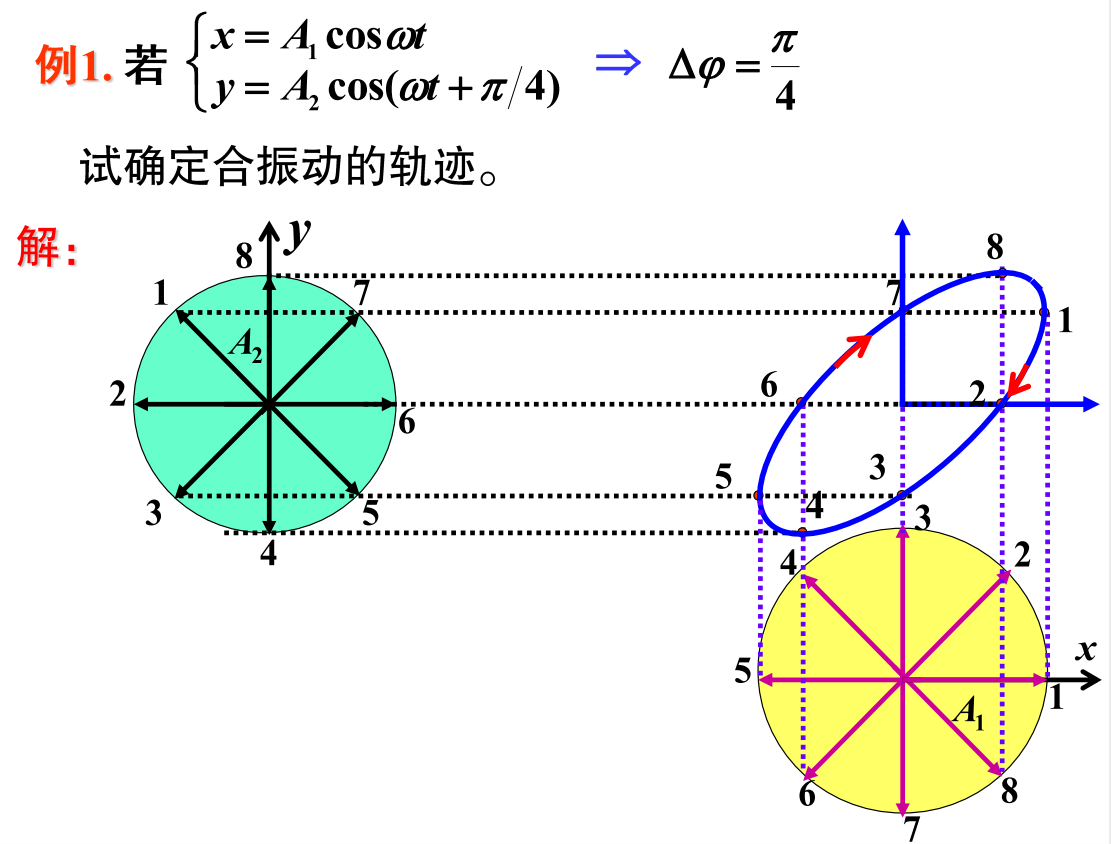
讨论\(\Delta \varphi\)
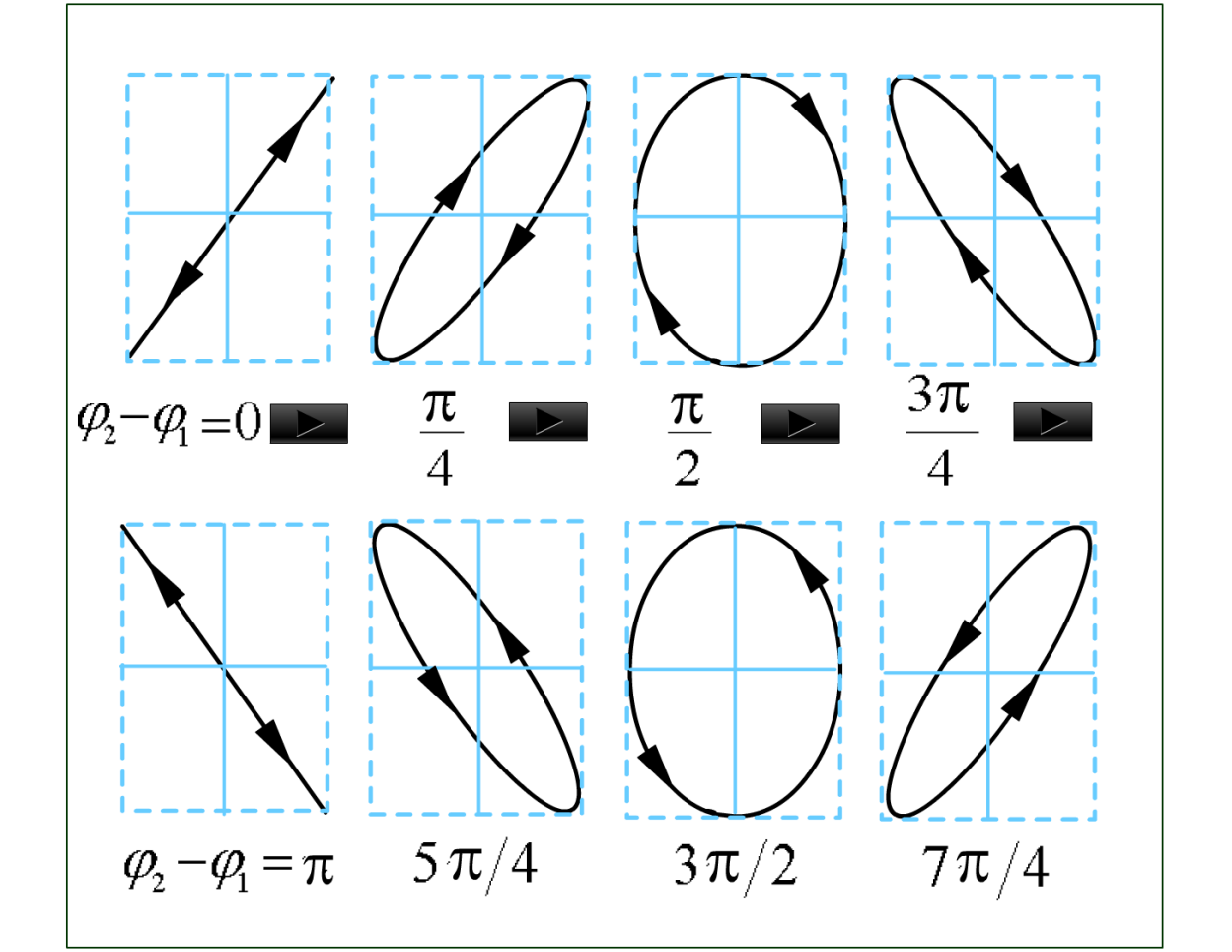
当\((\varphi_2-\varphi_1)=0/\pi\)时,为直线
当\((\varphi_2-\varphi_1)=\frac{1}{2}\pi/-\frac{1}{2}\pi\)时,为正椭圆
- 当\(A_1=A_2\)时,正椭圆为圆
相互垂直不同频率的简谐运动的合成
两分振幅频率相差很小
可近似看做两个频率相同,而\(\varphi_2-\varphi_1\)随t不断变化
\(\Delta\varphi\)从 \[ 0\to\frac{1}{2}\pi\to\pi\to\frac{3}{2}\pi\to2\pi \] 合运动轨迹\((0\sim \pi的情况)\)从
两振动的频率成整数比 \[ \frac{w_1}{w_2}=\frac{n}{m} \] 合成轨迹为稳定的闭合曲线--李萨如图形
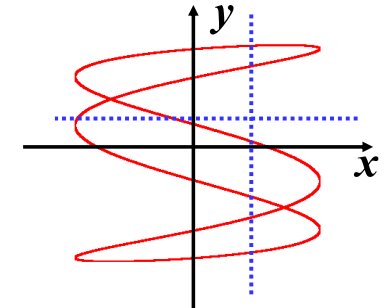
可以测量信号频率 \[ \frac{w_x}{w_y}=\frac{\nu_x}{\nu_y}=\frac{x出现的次数}{y出现的次数} \]
谐振分析
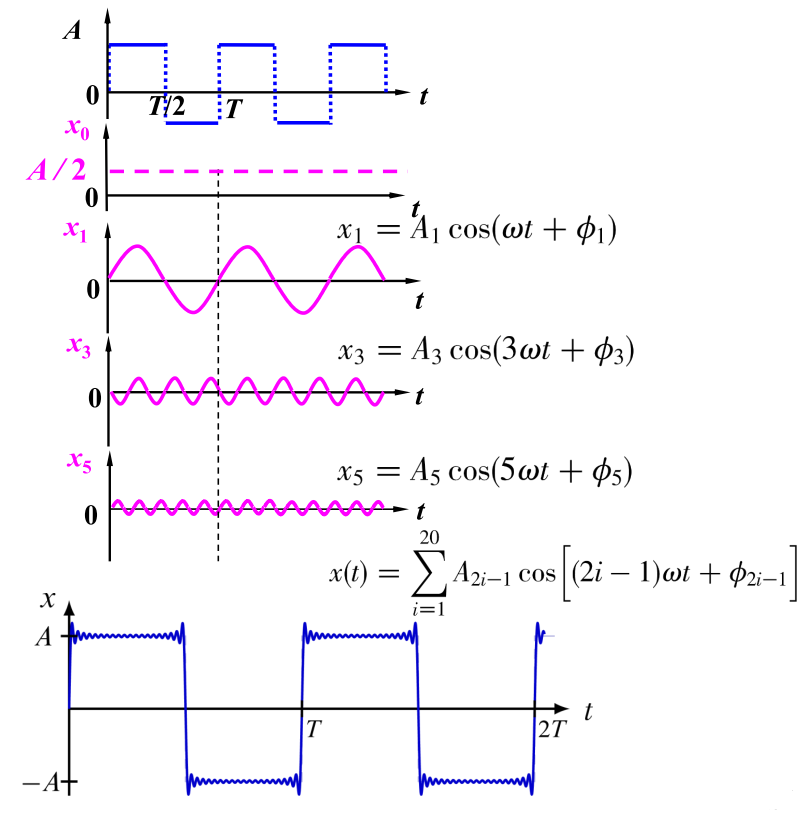
阻尼与受迫振动&共振
阻尼
动力学方程
\[ \frac{d^2x}{dt^2}+2\beta\frac{dx}{dt}+w_0^2x=0 \]
\[ w_0^2=\frac{k}{m},2\beta=\frac{\gamma}{m} \]
运动学特征
弱阻尼\(\beta<w_0\)

\[ w=\sqrt{w_0^2-\beta^2} \]
振幅随t按指数衰减
是准周期运动,出现两次极大的时间间隔 \[ T=\frac{2\pi}{w}=\frac{2\pi}{\sqrt{w_0^2-\beta^2}}>\frac{2\pi}{w_0}=T_0 \] 周期变长,振动变慢
能量E随振幅A的减小而衰减\(E\propto A^2\)
过阻尼\(\beta>w_0\)
- 非周期性运动
- 无振动发生
临界阻尼\(\beta=w_0\)
振子刚好处于一个从准周期振动转变到非周期运动的临界状态
受迫振动
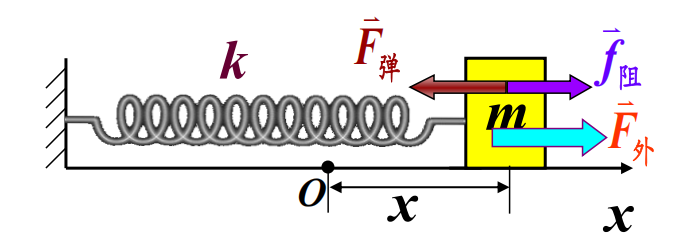
设强迫力为\(F(t)=F_m\cos wt\)
动力学方程
\[ \frac{d^2x}{dt^2}+2\beta\frac{dx}{dt}+w_0^2x=h\cos wt \]
\[ w_0^2=\frac{k}{m},2\beta=\frac{\gamma}{m},h=\frac{F_m}{m} \]
稳态时的受迫振动按简谐运动的规律变化,频率为\(w\)
将稳态方程带入解得: \[ 振幅:A=\frac{h}{\sqrt{(w_0^2-w^2)^2+4\beta^2w^2}} \]
\[ 相位:\tan\varphi=-\frac{2\beta w}{w_0^2-w^2} \]
稳定受迫振动和简谐振动的区别
受力不同
弹黄振子:
- \(w_0\)是系统固有的
- \(A,\psi\)取决于初始条件
受迫振动:
- \(w_0\)受外力影响
- \(A,\psi\)受外力和系统共同决定
简谐振动能量守恒
共振
\(\frac{dA}{dw}=0\)
共振频率为: \[ w_r=w=\sqrt{w_0^2-2\beta^2} \] 共振振幅为: \[ A_r=\frac{h}{2\beta\sqrt{w_0^2-\beta^2}} \] 若\(\beta \ll w_0\),则\(w_r\approx w_0,A_r=\frac{h}{2\beta}\),称为尖锐共振
当\(\beta\to 0\),即弱阻尼时,共振发生在固有频率处,称为尖锐共振
机械波
产生条件
- 波源
- 弹性介质:无穷多质点通过相互之间的弹性力作用组合在一起的连续介质。可以是固体、液体和气体。波源处质点的振动通过弹性介质中的弹性力,将振动状态在介质中由近及远地传播开去,从而形成机械波。
波的分类
横波:振动方向和传播方向垂直,如绳波,电磁波
- 有波峰,波谷,只存在于固体中
纵波:振动方向和传播方向相同,如声波
- 有疏密之分,存在于固液气中
波的描述
波的\(T\)和\(\nu\)取决于波源
波速\(u\)取决于介质(取决于介质的弹性模量和密度)
波长\(\lambda\)由波源和传输介质共同决定
平面简谐波
波源简谐振动,波面为平面
波函数
波源在o点,以速度u向x轴方向传播
在p点,振动时间比o点晚\(\frac{x}{u}\),相位比o点落后\(w\frac{x}{u}\)
p点t时刻振动位移为 \[ y=A\cos(wt-w\frac{x}{u}) \]
波函数的意义
x一定时,\(x=x_1\)为\(x_1\)处质点的振动方程
t一定时,\(t=t_1\)为\(t_1\)时刻波形方程
当\(x,t\)都不固定时,波函数描述了波形的传播
考察\(t_1\)和\(t_2=t_1+\Delta t\)时刻波形方程 \[ y_1=A\cos w(t_1-\frac{x}{u}) \] \[ y_2=A\cos w(t_2-\frac{x'}{u})=A\cos w(t1 + \Delta t-\frac{x'}{u})=A\cos (wt_1 - \frac{w(x'-u\Delta t)}{u}) \]
当\(x'=x + u\Delta t\)时,\(y_1=y_2\),说明经过\(\Delta t\)时间,整个波形向前平移了一段距离\(\Delta x=u\Delta t\)
一般形式
波源o初相位\(\psi\neq 0\),波源振动方程为\(y=\cos(wt+\varphi)\)
则p点振动方程为:
P点落后O点的相位:\(w\Delta t=wx/u\) \[ y=\cos(wt+(\varphi-wx/u)) \] P点落后O点的振动时间:\(\Delta t=x/u\) \[ y=\cos(w(t - x/u)+\varphi) \] 根据\(w=\frac{2\pi}{T}=2\pi\nu,u=\frac{\lambda}{T}=\lambda\nu\) \[ y=A\cos(wt-\frac{2\pi x}{\lambda}+\varphi) \] \[ y=A\cos[2\pi(\frac{t}{T}-\frac{x}{\lambda})+\varphi] \]
定义波数\(k=\frac{2\pi}{\lambda}\) \[ y(x,t)=A\cos((wt-kx)+\varphi)=Ae^{i(wt-kx)+i\varphi} \] 相位差: \[ \Delta \varphi=k\Delta x \]
波反向传播

波的能量
波的能量的传播
在\(x\)处取长度为\(\Delta x\),体积为\(\Delta V=S\Delta x\),质量为\(\Delta m=\rho\Delta V\)
振动动能 \[ E_k=\frac{1}{2}\rho\Delta VA^2w^2\sin^2w(t-\frac{x}{u}) \]
振动势能 \[ E_p=\frac{1}{2}\rho\Delta VA^2w^2\sin^2w(t-\frac{x}{u}) \] t时刻质元的总能量 \[ E=\rho\Delta VA^2w^2\sin^2w(t-\frac{x}{u}) \] 体积元中动能和势能同相地随时间变化,在任一时刻都具有相同的数值
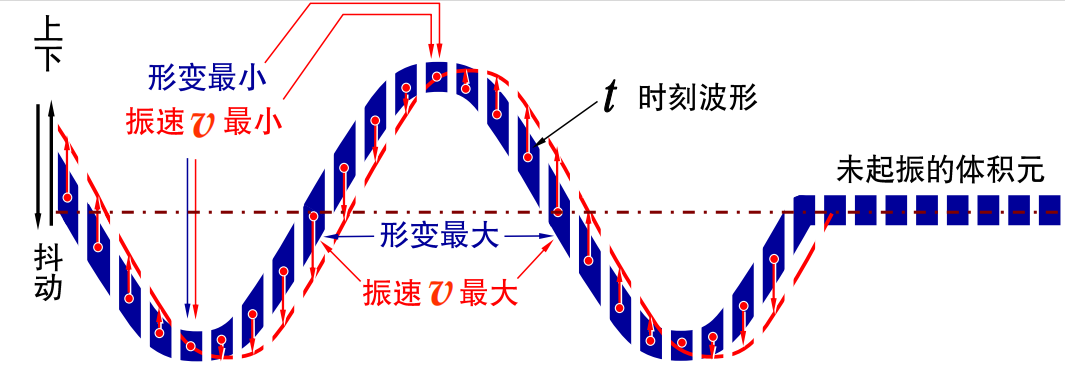
能量密度
能量密度: \[ w=\frac{\Delta W}{\Delta V}=\rho A^2w^2\sin^2w(t-\frac{x}{u}) \] 周期 \[ T'=\frac{1}{2}T \] 平均能量密度: \[ \bar{w}=\frac{1}{2}\rho A^2w^2 \] 平面简谐波在各处的平均能量密度都相等
介质并不积累能量,能量随着波动的行进,从介质的这一部分传到另一部分。波动是能量传播的一种形式;波动的能量沿波速方向传播
能流密度
能流 P:单位时间内垂直通过某一截面的能量
\(\Delta t\)时间内通过垂直于波速截面\(\Delta S\)的能量,\(\Delta W=u\Delta t\Delta Sw\),\(w\)是截面所在的能量密度 \[ P=\frac{\Delta W}{\Delta t}=u\Delta S w=u\Delta S\rho A^2w^2\sin^2w(t-\frac{x}{u}) \] 平均能流:在一个周期内能流的平均值 \[ \bar{P}=u\Delta S \bar w=\frac{1}{2}\rho A^2w^2u\Delta S \] 能流密度\(i\)是单位时间内通过垂直于波速方向的单位面积的能量。 \[ i=wu \] 平均能流密度:通过垂直于波动传播方向的单位面积的平均能流,又称为波的强度,单位\(W/m^2\) \[ I=\frac{\bar P}{\Delta S}=u\bar w=\frac{1}{2}\rho A^2w^2u \] 矢量表示,方向和u相同 \[ \vec{I}=\frac{1}{2}\rho A^2w^2\vec u \] 穿过各波面的平均能流应相等


衍射&干涉
干涉
相干条件:
- 频率相同
- 振动方向相同
- 相位差恒定
两波源\(S_1,S_2\)振动表达式为: \[ y_{10}=A_1\cos(wt+\varphi_{10}) \] \[ y_{20}=A_2\cos(wt+\varphi_{20}) \]
传播到p点引起的振动为: \[ y_{1}=A_1\cos(wt+\varphi_{10}-\frac{2\pi}{\lambda}r_1) \] \[ y_{2}=A_2\cos(wt+\varphi_{20}-\frac{2\pi}{\lambda}r_2) \]
两分振动相位差为: \[ \Delta \varphi=(\varphi_{20}-\varphi_{10})-\frac{2\pi}{\lambda}(r_2-r_1) \]
驻波
振幅、频率、传播速度都相同的两列相干波,在同一直线上沿相反方向传播时叠加而形成的一种特殊的干涉现象。
设有两列相干波,分别沿x轴正、负方向传播,选初相位均为零的表达式为: \[ y_1=A\cos(wt-\frac{2\pi}{\lambda}x),y_2=A\cos(wt+\frac{2\pi}{\lambda}x) \] \[ y=y_1+y_2=2A\cos\frac{2\pi}{\lambda}x\cdot\cos wt \]
特点:
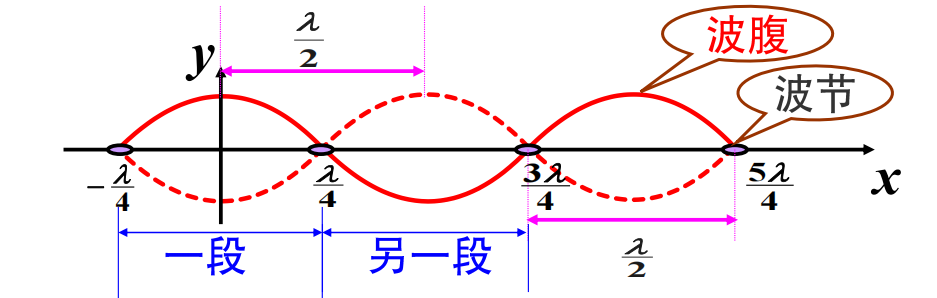
振幅呈周期性分布: \[ |2A\cos\frac{2\pi}{\lambda}x| \] 振幅最大的称为波腹: \[ x=k\frac{\lambda}{2} \] 振幅最小的称为波节: \[ x=(2k+1)\frac{\lambda}{4} \]
两个波节之间一段中的各点振动位相相同,在波节两侧的点(邻近两段)振动位相相反
驻波不传播能量
- 驻波的动能主要集中在波腹,势能主要集中在波节。能量在相邻的波腹和波节间往复变化
- 驻波中没有振动状态或位相的传播,也没有能量的传播,实际上是分段振动
- 驻波不是波动,而是一种特殊形式的振动
弦线上的驻波
一弦线两段固定,两端点为波节
可能驻波长: \[ L=n\frac{\lambda}{2},n=1,2,3,... \]
半波损失
\(\rho u\)大的是波密,\(\rho u\)小的是波疏
从光疏射向光密的反射光有半波损失
多普勒效应
波源和接收器都静止\(v_s=0,v_R=0\) \[ v1=v \] 波源静止,接收器运动\(v_s=0,v_R\neq 0\) \[ 靠近:v_2=\frac{u+v_R}{u}v \] \[ 远离:v_2=\frac{u-v_R}{u}v \]
波源运动,接收器静止\(v_s\neq 0,v_R=0\) \[ 靠近:v_3=\frac{u}{u-v_s}v \] \[ 远离:v_3=\frac{u}{u+v_s}v \]
两个都运动:
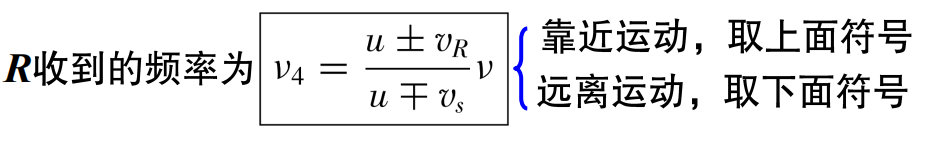
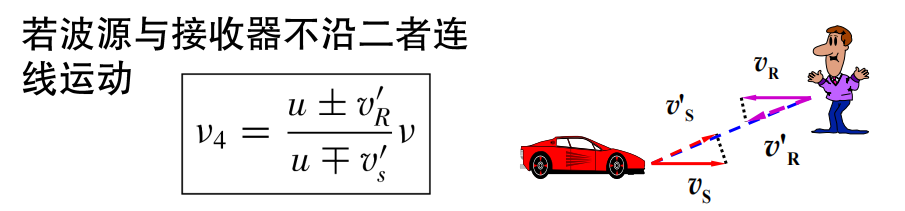
冲击波和马赫锥
若波源速度超过波速,\(v_s\gg u\),各时刻波源发出波的波前的包络面为一个以波源为顶点的圆锥面
马赫锥的半顶角: \[ \sin\alpha=\frac{u}{v_s}=\frac{1}{M} \] 当\(u=v_s\)时,马赫锥的半顶角为\(\frac{\pi}{2}\)
电磁震荡和电磁波
电磁震荡
LC电路,无阻尼振荡:电路中电量和电流的周期性变化
产生的电磁振荡是无阻尼自由振荡
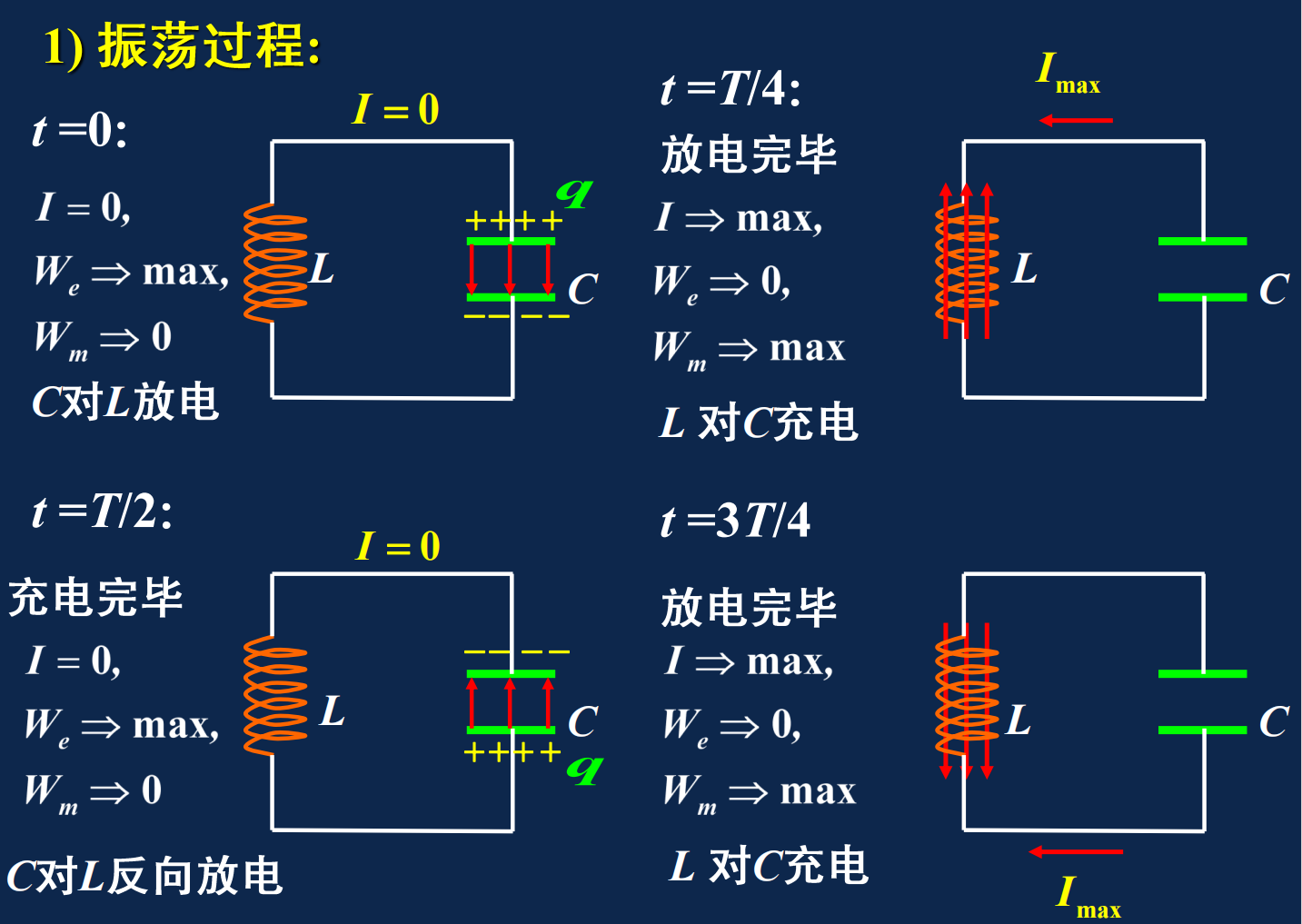
与简谐振动对比

电量随时间变化: \[ q=Q_0\cos(wt+\varphi) \] 电流随时间变化: \[ i=-wQ_0\sin(wt+\varphi)=I_0\cos(wt+\varphi+\frac{\pi}{2}) \] LC振荡频率: \[ w=\sqrt{\frac{1}{LC}} \]
\[ C=\frac{\varepsilon S}{d},L\propto N^2 \]
电磁波的发射和传播
变化的磁场和变化的电场互相激发形成电磁波
赫兹实验
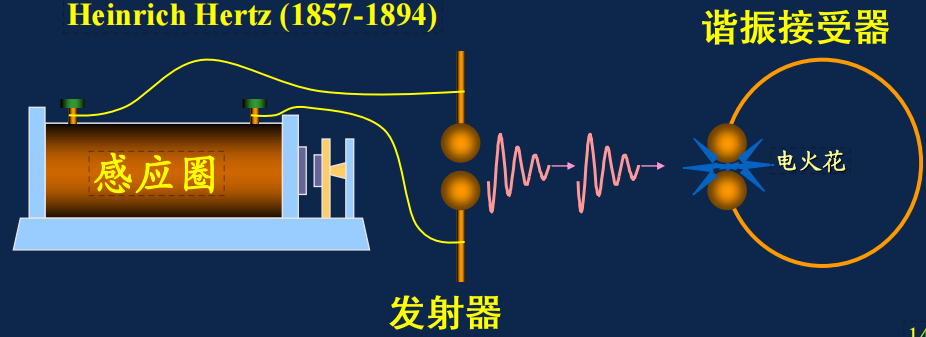
假设两根导体棒水平,在导体棒接上高压电之后:
产生的电场和磁场相互垂直,电场水平,磁场垂直
平面电磁波
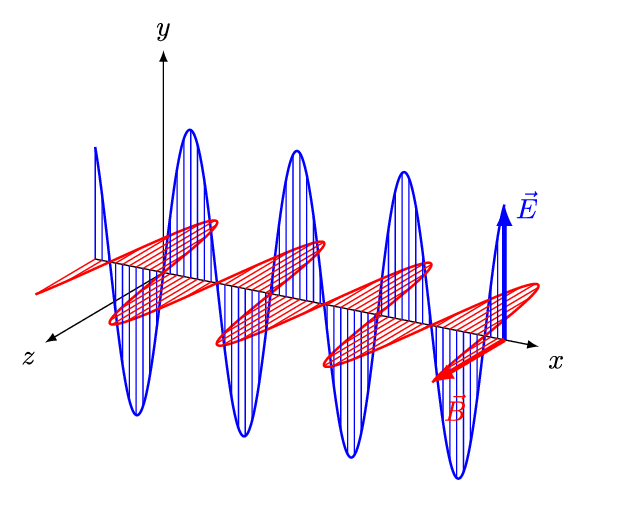
理论和实践都证明:若\(E\)在\(y\)方向振动,则\(B\)在\(z\)方向振动,电磁波沿\(x\)方向传播。(满足右手螺旋)
波动方程: \[ \frac{\partial ^2 E}{\partial t^2}=\frac{1}{\varepsilon \mu}\frac{\partial ^2 E}{\partial x^2} \]
\[ \frac{\partial ^2 H}{\partial t^2}=\frac{1}{\varepsilon \mu}\frac{\partial ^2 H}{\partial x^2} \]
电磁波波速为: \[ u=\frac{1}{\sqrt {\varepsilon \mu}} \] 当电磁波波动方程中沿\(x\)轴正向传播的平面余弦波特解为: \[ E_y=E_{y0}\cos[w(t-\frac{x}{u})+\varphi] \] 相应地磁场部分为: \[ H_z=H_{z0}\cos[w(t-\frac{x}{u})+\varphi] \] \(H\)的振幅: \[ H_{z0}=\frac{E_{y0}}{\mu u}=\sqrt{\frac{\varepsilon}{\mu}}E_0或\sqrt{\varepsilon}E_{y0}=\sqrt{\mu}H_{z0} \]
电磁波的能量
电场能量密度: \[ w_e=\frac{1}{2}\varepsilon E^2 \] 磁场能量密度: \[ w_m=\frac{1}{2}\mu H^2=\frac{1}{2}\varepsilon E^2 \] 总能量密度: \[ w=w_e+w_m=\frac{1}{2}(\varepsilon E^2+\mu H^2)=\varepsilon E^2=\mu H^2=\sqrt{\varepsilon \mu}EH=\frac{1}{u}EH \] 能流密度:单位时间内垂直通过单位面积的电磁能量 \[ S=wu=EH \] 能流密度矢量(坡印亭矢量): \[ \vec{S}=\vec{E}\times \vec{H} \] 平均能流密度(电磁波强度): \[ I=\bar{S}=\frac{1}{2}E_0H_0 \] 因为\(\sqrt{\varepsilon}E_{y0}=\sqrt{\mu}H_{z0}\) 和 \(c=\frac{1}{\sqrt{\varepsilon_0\mu_0}}\) \[ \bar{S}=\frac{1}{2}\varepsilon_0cE_0^2=\frac{1}{2}\mu_0cH_0^2 \]














