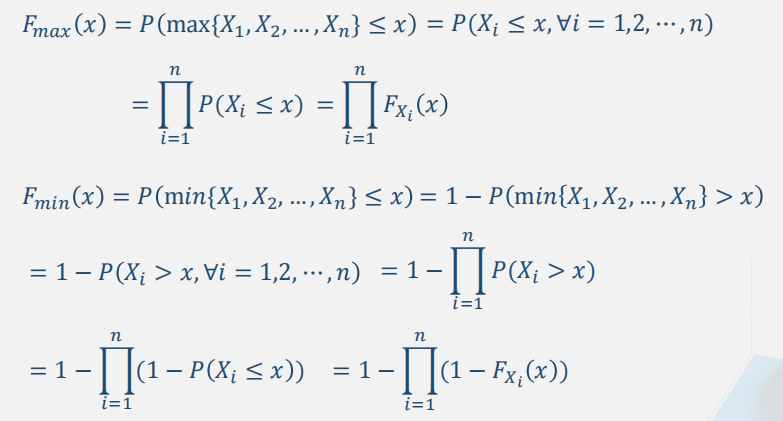多维随机变量

联合分布函数： \[ F(x,y)=P(X\leq x,Y\leq y) \] 边缘分布函数： \[ F_X(x) = F(x,+\infty) \]

\[ F_Y(y) =F(+\infty,y) \]

离散型

当\(p_{i\cdot}\neq0\)或\(p_{\cdot j}\neq0\)时我们可以由条件概率的乘积公式计算\(p_{ij}\)

连续型

若存在二元非负函数\(f(x,y)\)使得二维随机变量\((X,Y)\)的分布函数 \[ F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^yf(u,v)dudv \] 则称\((X,Y)\)为一二维连续型随机变量，\(f(x,y)\)为\((X,Y)\)的联合概率密度

边缘概率密度： \[ f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy \]

\[ f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)dx \]

常用二维连续型随机变量

二维均匀分布\((X,Y)\sim U(D)\)

若\(D\subset R^2\)，且面积\(0<m(D)<+\infty\)，则称具有概率密度 \[ f(x,y)=\left\{\begin{matrix} 1/m(D) &(x,y)\in D \\ 0&(x,y)\not\in D \end{matrix}\right. \] 多维均匀分布的边缘分布不一定是一维均匀分布

二维正态分布\((X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)\)

密度： \[ f(x) = \frac{1}{2\pi \sigma_1 \sigma_2 \sqrt{1 - \rho^2}} \exp\left(-\frac{1}{2(1 - \rho^2)} \left( \frac{(x - \mu_1)^2}{\sigma_1^2} - \frac{2\rho (x - \mu_1)(y - \mu_2)}{\sigma_1 \sigma_2} + \frac{(y - \mu_2)^2}{\sigma_2^2} \right)\right) \] 边缘分布： \[ X\sim N(\mu_1,\sigma_1^2) \] \[ Y\sim N(\mu_2,\sigma_2^2) \]

多维正态分布的边缘分布仍为正态分布

条件分布

离散型

直接用条件概率求解即可

连续型

已知\(X=x\)时Y的条件概率密度： \[ f(y|x)=\frac{f(x,y)}{f_X(x)} \] 全概率公式： \[ f_Y(y)=\int_{-\infty}^{+\infty}f_X(x)f(y|x)dx \] \[ f_X(x)=\int_{-\infty}^{+\infty}f_Y(y)f(x|y)dy \]

若\((x,y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_1^2,\rho)\)，则在已知\(Y=y\)的条件下，X服从正态分布 \[ N(\mu_1+\frac{\sigma_1}{\sigma_2}\rho(x-\mu_1),(1-\rho^2)\sigma_2^2) \]

随机变量的独立性

若\((X_1,X_2,...,X_n)\)为连续型随机变量，则\(X_1,X_2,...,X_n\)相互独立当且仅当 \[ f(x_1,x_2,...,x_n)=\prod_{i=1}^{n}f_{X_i}(x_i) \]
若\(X_1,X_2,...,X_n\)相互独立，则对于n个函数\(g_1,g_2,...,g_n\)，\(g_1(X_1),g_2(X_2),...,g_n(X_n)\)相互独立

对于二维正态分布\((x,y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_1^2,\rho)\)，\(X,Y\)独立的充分必要条件是\(\rho=0\)

多维随机变量函数的分布

离散型

直接计算其分布列即可

实例

\(X,Y\)独立，\(X\sim B(m,p)\)，\(Y\sim B(n,p)\)，则 \[ X+Y\sim(m+n,p) \]

连续型

先求分布函数，如果Y为一连续随机变量，则求导得其概率密度

和的分布

设\((X,Y)\)的联合密度为\(f(x,y)\)，\(Z=X+Y\)，积分区域为\(x + y\leq z\)，则Z的分布函数为 \[ F_Z(z)=\int_{-\infty}^{+\infty}dy\int_{-\infty}^{z-y}f(x,y)dx \] 概率密度： \[ f_Z(z)=\int_{-\infty}^{+\infty}f(x,z-x)dx=\int_{-\infty}^{+\infty}f(z-y,y)dy \] 若\(X,Y\)独立 \[ f_Z(z)=\int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)dx=\int_{-\infty}^{+\infty}f_X(z-y)f_Y(y)dy \] 实例

若\(X_1,...,X_n\)相互独立，且\(X_i\sim N(\,u_i,\sigma_i^2)\)，则 \[ \sum_{i=1}^{n}a_iX_i\sim N(\sum_{i=1}^{n}a_i\mu_i,\sum_{i=1}^{n}a_i^2\sigma_i^2) \]

\[ X_1-X_2\sim N(\mu_1-\mu_2,\sigma_1^2{\color\red{+}}\sigma_2^2) \]

\(X\sim P(\lambda_1),Y\sim P(\lambda_2)\) \[ X+Y\sim P(\lambda_1+\lambda_2) \]