量子力学
德布罗意波
德布罗意关系式
\[ E=h\nu \]
\[ P=\frac{h}{\lambda} \]
实验验证
戴维逊—革末电子衍射实验

不确定关系
概念:微观粒子的位置(坐标)和动量不能同时具有确定的值
在某确定方向上(如x方向)粒子的位置有不确定量\(\Delta x\),对应动量的不确定量\(\Delta p\),二者有一关系 \[ \Delta x\cdot\Delta p_x\geq \frac{\hbar}{2} \] \(\Delta x\)是位置标准差,\(\Delta px\)是动量标准差,\(\hbar\)是约化普朗克常数,其中\(\hbar=\frac{h}{2\pi}\)
以单缝衍射为例

波函数
微观粒子状态描述--波函数
一维无限深势阱中粒子的波函数: \[ \large\Psi(x,t)=\Psi_0e^{-\frac{i}{\hbar}(Et-px)} \] 扩展到三维空间: \[ \large\Psi(r,t)=\Psi_0e^{-\frac{i}{\hbar}(Et-pr)} \]
量子力学基本假设
- 一个系统的状态可以用一个波函数完全描述。该波函数包含了该系统处于该状态时的所有物理信息。
- 如果\(\Psi_1,\Psi_2\)是两个可能的状态,那么\(\Psi=c_1\Psi_1+c_2\Psi_2\)也是一个可能的状态
叠加态的意义:如果粒子处于上述叠加态,它同时处于\(\Psi_1\)和\(\Psi_2\)表示的状态
概率解释
电子出现在x附近的单位区间内的概率(密度)为 \[ \rho(x,t)=\frac{dP}{dx}=|\Psi(x,t)|^2 \] 推广到三维的情况,粒子出现在\(x\to x+dx,y\to y+dy,z\to z+dz\)的概率为 \[ \rho(r,t)=\frac{dP}{dxdydz}=|\Psi(r,t)|^2 \]
物理意义
波函数本身表示了微观粒子的波动性,而它的模的绝对值的平方又描述了微观粒子的空间位置概率分布(粒子性)
定态波函数:定态波函数的概率密度不随时间变化,能量取确定值 \[ \Psi_E(x,t)=\psi_E(x)e^{-iEt/{\hbar}} \]
\[ |\Psi_E|^2=|\psi_E(x)|^2 \]
- 已知波函数可求动量、动能、能量以及角动量等、力学量的概率分布,进而可求它们的平均值。
归一化条件
未归一化的波函数: \[ \int_{-\infty}^{+\infty}|\Psi(r,t)|^2dV=N \] 归一化: \[ \tilde{\Psi}(r,t)=\frac{1}{\sqrt{N}}\Psi(r,t) \]
自由粒子的波函数
自由粒子:不受任何外力作用,也不处在任何外力场中 \[ \left\{\begin{matrix} E=恒量& E=h\nu=\hbar\omega &\nu或\omega 恒定\\ \vec{p}=恒量& p=\frac{h}{\lambda}=\hbar\vec k &p=\hbar\vec k 恒定 \end{matrix}\right. \] 描述自由粒子的单色平面波: \[ \Psi(\vec{r},t)=Ae^{-\frac{i}{\hbar}(Et-\vec{p}\vec{r})} \] 粒子出现在空间x点的概率密度: \[ \rho(x)=|\Psi(x,t)|^2=\psi_0^2e^{-\frac{i}{\hbar}(Et-\vec{p}\vec{r})}e^{\frac{i}{\hbar}(Et-\vec{p}\vec{r})}=\psi_0^2 \] 根据上式,自由粒子在各点概率相等,即自由粒子位置完全不确定
薛定谔方程
自由粒子薛定谔方程
一维运动自由粒子含时的薛定谔方程: \[ -\frac{\hbar^2}{2m}\frac{\partial ^2\Psi}{\partial x^2}=i\hbar\frac{\partial \Psi}{\partial t} \] 如果粒子在三维空间: \[ -\frac{\hbar}{2m}\nabla^2\Psi=i\hbar\frac{\partial\Psi}{\partial t} \] 其中拉普拉斯运算符\(\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\)
势场中粒子的薛定谔方程
\[ i \hbar \frac{\partial}{\partial t} \psi(\mathbf{r}, t) = \left( -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}, t) \right) \psi(\mathbf{r}, t) \]
- 是量子力学的基本方程,描述非相对论粒子波函数随时间演化规律
- 是线性齐次微分方程,满足叠加态原理
- 方程中含有虚数i,它的解\(\Psi\)是复函数,复数不能直接测量,但是\(\Psi\)的模方代表概率密度,可测量
定态薛定谔方程
当势能\(V=V(x)\)不显含时间而只是坐标的函数时,薛定谔方程的解可用分离变量法进行简化,用定态薛定谔方程描述。
定态薛定谔方程描述的是时间独立的情况下粒子的量子状态。它的形式为:
\[ \hat{H} \psi(\mathbf{r}) = E \psi(\mathbf{r}) \]
其中,\(\hat{H}\) 是哈密顿算符,\(\psi(\mathbf{r})\) 是粒子的空间波函数,\(E\) 是粒子的能量本征值(满足方程的E值)。
哈密顿算符通常包含动能和势能项:
\[ \hat{H} = -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}) \]
因此,定态薛定谔方程可以写为:
\[ -\frac{\hbar^2}{2m} \nabla^2 \psi(\mathbf{r}) + V(\mathbf{r}) \psi(\mathbf{r}) = E \psi(\mathbf{r}) \]
其中,\(\nabla^2\) 是拉普拉斯算符,\(V(\mathbf{r})\) 是势能函数,\(\psi(\mathbf{r})\) 是空间波函数。
薛定谔方程的特解(总的波函数)为: \[ \psi(\mathbf{r}, t) = \psi_E(\mathbf{r}) e^{-i \frac{E t}{\hbar}} \] 粒子位置的概率密度为 \[ |\psi(\mathbf{r}, t)|^2=|\psi_E(\mathbf{r})|^2 \]
一维定态薛定谔方程的应用
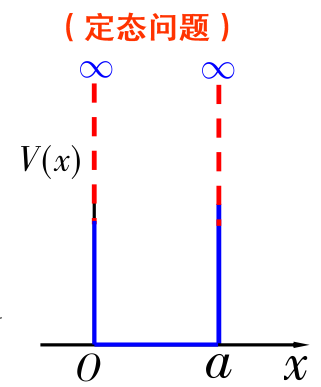
一维无限深势阱
波函数
 \[
\left\{\begin{matrix}
V(x)=0 & 0<x<a \\
V(x)=\infty & x\leq0,x\geq a
\end{matrix}\right.
\] 在阱外:由于\(V\to
\infty\),对于能量\(E\)有限的粒子没有可能性到达阱外,所以在\(x\leq 0\)和\(x\geq a\)的区域,\(\Psi = 0\)
\[
\left\{\begin{matrix}
V(x)=0 & 0<x<a \\
V(x)=\infty & x\leq0,x\geq a
\end{matrix}\right.
\] 在阱外:由于\(V\to
\infty\),对于能量\(E\)有限的粒子没有可能性到达阱外,所以在\(x\leq 0\)和\(x\geq a\)的区域,\(\Psi = 0\)
在阱内:由于\(V=0\),设波函数为\(\Psi\)
定态薛定谔方程为 \[ \frac{d^2\Psi}{dx^2}+\frac{2mE}{\hbar^2}\Psi=0 \] 令 \[ k^2=\frac{2mE}{\hbar^2} \] 则上式变成 \[ \frac{d^2\Psi}{dx^2}+k^2\Psi=0 \] 最终解得
k只能取一系列分立的值 \[ k=\sqrt{\frac{2mE}{\hbar^2}}=\frac{n\pi}{a}(n=1,2,...) \] 粒子能量只能取分立的值 \[ E=n^2E_1(n=1,2,...) \] \[ E_1=\frac{\pi^2\hbar^2}{2ma^2} \]
阱内的波函数为 \[ \Psi(x)=A\sin\frac{n\pi x}{a} \] 由归一性条件得 \[ A=\sqrt\frac{2}{a} \] 总结:势阱内粒子的定态波函数为 \[ \Psi_n(x)=\left\{\begin{matrix} \sqrt\frac{2}{a} \sin\frac{n\pi x}{a}&(n=1,2,...)&0<x<a \\ 0&&x\leq0,x\geq a \end{matrix}\right. \]
运动特征
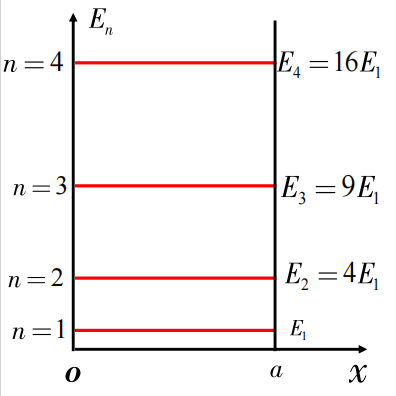
能量是量子化的 \[ E=n^2\frac{\pi^2\hbar^2}{2ma^2},n=1,2,... \] 每一个能量值对应一个能级
相邻两个能级的间隔: \[ \Delta E=(2n+1)\frac{\pi^2\hbar^2}{2ma^2} \left\{\begin{matrix} n\uparrow,\Delta E\uparrow \\ a\downarrow,\Delta E\uparrow \end{matrix}\right. \]
- 当势阱宽度a小到原子尺度,能级差很大,能量的量子化显著
- 当势阱宽度a大到宏观的尺度,能级差很小,能量量子化不显著。可把能量看成连续,回到了经典理论
势阱中粒子最低能量不为零 \[ E=n^2E_1(n=1,2,...) \] \[ E_1=\frac{\pi^2\hbar^2}{2ma^2}\rightarrow动能,因为V=0 \]
量子理论认为势阱中粒子的能量不可能为零,即粒子 不可能在阱内静止
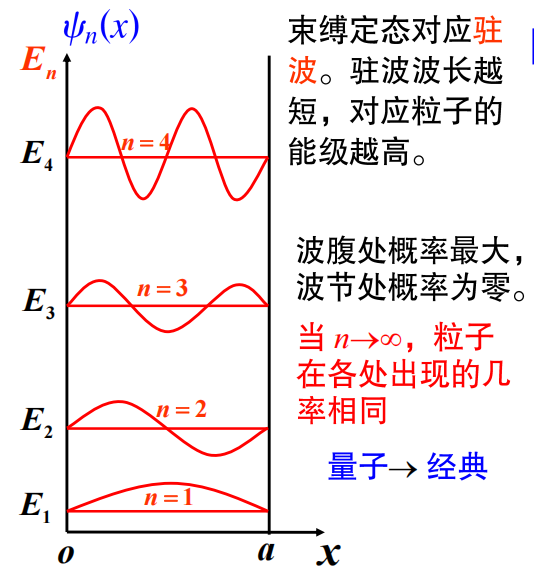
势阱中粒子的德布罗意波 \[ p_n=\sqrt{2mE_n}=\frac{n\pi\hbar}{a}=\frac{h}{\lambda_n} \] \[ \lambda_n=\frac{2a}{n} \]
能量\(E_n\)的定态\(\Psi_n\),对应波长为\(\lambda_n\)的德布罗意波的驻波
对不同的n可得到粒子的能级图
 \[
\Delta E=(2n+1)\frac{\pi^2\hbar^2}{2ma^2}
\] 当\(n\to\infty\)时 \[
\frac{\Delta E}{E_n}=\frac{2n+1}{n^2}\Rightarrow 0
\] 在高能级上可看成能级连续分布
\[
\Delta E=(2n+1)\frac{\pi^2\hbar^2}{2ma^2}
\] 当\(n\to\infty\)时 \[
\frac{\Delta E}{E_n}=\frac{2n+1}{n^2}\Rightarrow 0
\] 在高能级上可看成能级连续分布粒子在势阱中出现的概率\(|\Psi_n(x)|^2\) \[ \Psi_n(x)=\sqrt\frac{2}{a} \sin\frac{n\pi x}{a} \]
一维势垒
势垒的势能函数
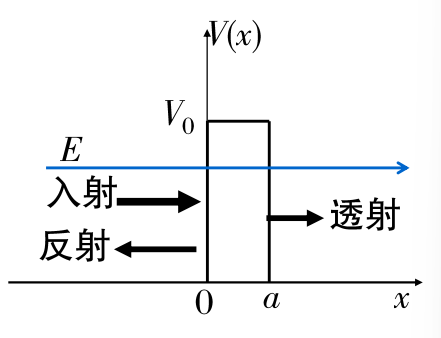 \[
V(x)=\left\{\begin{matrix}
V_0 &0\leq x \leq a\ \\
0& x<0,x>a
\end{matrix}\right.
\] 透射率:粒子穿过势垒的几率 \[
T\approx \large e^{[-\frac{2{\color{red} a} }{\hbar}\sqrt{2{\color{red}
m} (V_0-E)}]}
\]
粒子容易穿透薄的势垒,质量小的粒子穿透势垒的几率大
\[
V(x)=\left\{\begin{matrix}
V_0 &0\leq x \leq a\ \\
0& x<0,x>a
\end{matrix}\right.
\] 透射率:粒子穿过势垒的几率 \[
T\approx \large e^{[-\frac{2{\color{red} a} }{\hbar}\sqrt{2{\color{red}
m} (V_0-E)}]}
\]
粒子容易穿透薄的势垒,质量小的粒子穿透势垒的几率大
用量子力学处理氢原子问题
氢原子的薛定谔方程及其解
核外电子在核电荷的势场中: \[ V_\infty=0\\ V=-\frac{e^2}{4\pi\varepsilon_0r} \] 定态薛定谔方程:
上述方程的解可以写成:
电子波函数及氢原子的特征:
能量量子化 \[ E_n=-\frac{me^4}{8\varepsilon_0^2h^2}\frac{1}{n^2},n=1,2,3,... \] n维主量子数,\(E_n\)与波尔理论一致
角动量量子化 \[ L=\sqrt{l(l+1)}\hbar \] \(l\)是角量子数,L共有n个值
但是波尔理论中\(L=n\hbar\)

角动量的空间量子化
角动量的z分量为 \[ L_z=\sqrt{l(l+1)}\hbar\ (l=0,1,2,...,n-1) \]
当n一定时,\(l\)可取\(0,1,2,...,n-1\)与之对应,即同一个能级有n个不同大小的电子轨道角动量与之对应。
对于每一个\(l\),轨道角动量的大小为\(L=\sqrt{l(l+1)}\hbar\),但其方向由\(m_l\)确定,\(m_l=0,\pm 1,\pm 2,...,\pm l\)即有\(2l+1\)个不同的轨道角动量的空间取向对应同一个大小的轨道角动量
即对于一个确定的n,可存在的不同状态数为 \[ \sum_{l=0}^{n-1}(2l+1)=n^2 \]
波函数及电子的位置概率分布
\[ dP=(|rR_{n,l}|^2dr)\cdot(|Y_{l,ml}\sin \theta d\theta d \varphi|) \]
径向几率
在半径\(r\)到\(r+dr\)的球壳内找到电子的概率: \[ \rho_{nl}(r)=r^2R_{n,l}^2 \]
角向概率
电子在\((\theta,\varphi)\)附近的立体角\(d\Omega\)的概率: \[ \rho_{lm_l}(\theta,\varphi)d\Omega=|Y_{l,ml}|^2d\Omega \]
综述
描述氢原子运动状态的波函数为: \[ \Psi_{nlm_l}(r,\theta,\varphi)=R_{nl}(r)Y_{l,m_l}(\theta,\varphi) \] 它可以用三个量子数\((n,l,m_l)\)确定
- 主量子数\(n=1,2,3,...\),决定电子的能量\(E_n=-\frac{me^4}{8\varepsilon_0^2h^2}\frac{1}{n^2}\)
- 角量子数\(l=0,1,2,..,n-1\),决定电子轨道角动量大小\(L=\sqrt{l(l+1)\hbar}\)
- 轨道磁电子数\(m_l=0,\pm1,...,\pm l\),决定轨道角动量的空间取向\(L_z=m_l\hbar\)
电子自旋
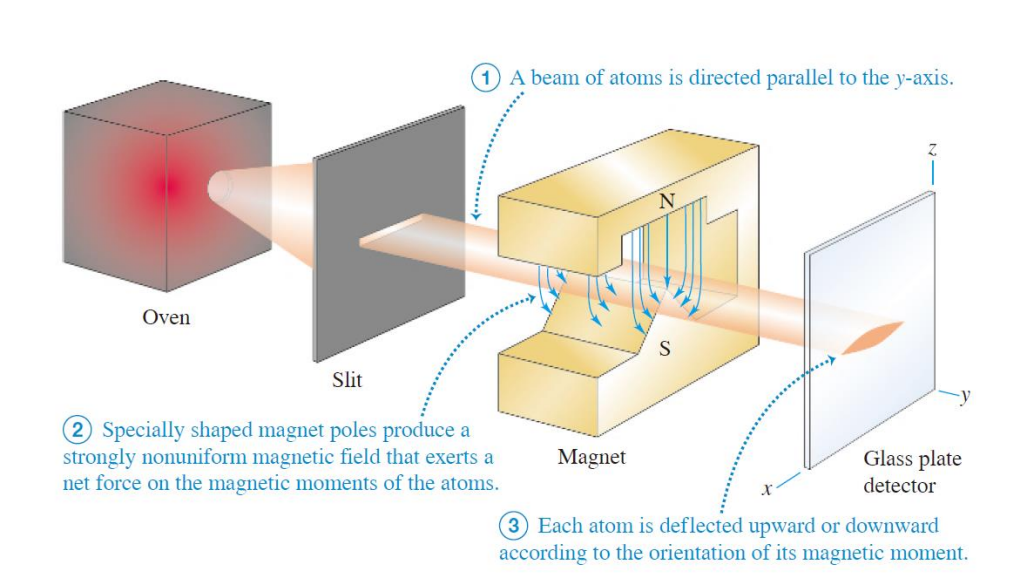
施特恩-格拉赫实验
目的:验证电子角动量的空间量子化
过程:让\(l=0\)的银原子通过非均匀磁场
结果:原子束的轨迹发生偏转,得到两条分开的径迹,分开的距离关于中心对称
分析:因为\(l=0\)所以角动\(L=0\),轨道运动产生的磁矩\(\mu_i=0\),所以这些原子经过不均匀磁场时不受力,所以必有其他磁矩或者角动量影响偏转
电子自旋
电子自旋角动量\(L_s\),s称为自旋量子数,只能取\(\frac{1}{2}\) \[ L_s=\sqrt{s(s+1)\hbar},s=\frac{1}{2} \]
\(L_s\)在任意方向的投影值只有两个
\(L_{s,z}=m_s\hbar,m_s=\pm\frac{1}{2}\)

原子电子壳层结构
泡利不相容原理
在原子中,不可能有四个量子数\(n,l,m_l,m_s\)完全相同的两个或两个以上的电子。
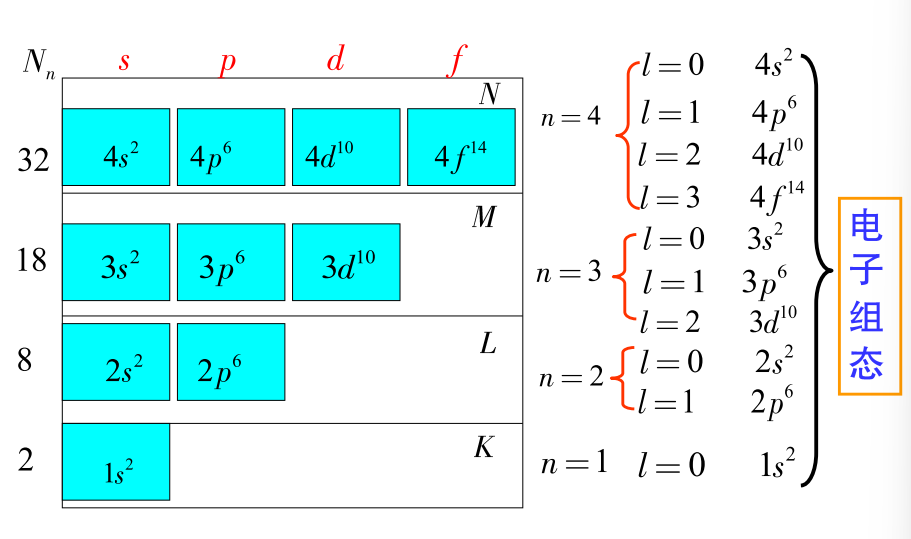
原子中具有相同主量子数n的电子数目最多为 \[ Z_n= \sum\limits_{l=0}^{n-1}2(2l+1)=2n^2 \] 主量子数n相同的电子位于同一壳层
- 对应\(n=1,2,3,...\)的壳层分别用\(K,L,M,...\)表示
在一个壳层内,按不同的角量子数\(l\),分成若干次壳层
- 主量子数为n的壳层包含n个次壳层,对应\(l=0,1,2,3,4,5,...\)用\(s,p,d,f,g,h,...\)表示
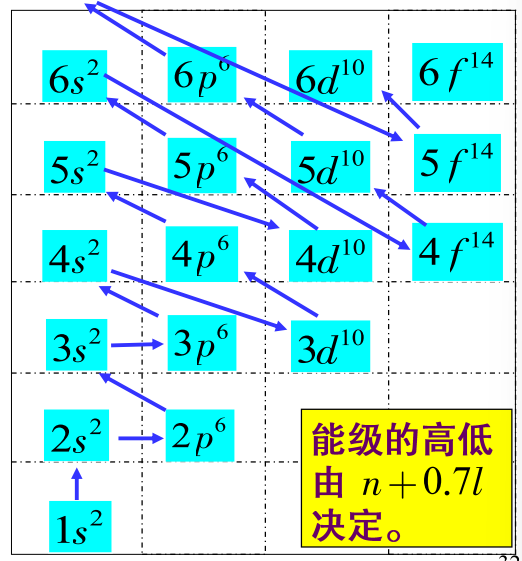
能量最小原理
电子填充壳层的次序总是每个电子趋向于占有最低的能级。