早期量子论
黑体辐射
概念
辐出度\(M(T)\ W/m^2\):温度为T的物体表面,单位时间内、单位面积上所发射的各种波长的电磁波能量总和
单色辐出度\(M(\lambda, T)=\frac{dM(T)}{d\lambda}\ W/m^3\):温度为T的物体表面,单位时间内、单位面积上所发射的波长在\(\lambda\)附近单位波长间隔内电磁波的能量
在一定温度时,物体的辐出度与单色辐出度有如下关系: \[ M(t) = \int_0^{\infty}M(\lambda,T)d\lambda \] 黑体:在任何温度下只吸收而不反射任何电磁波的物体
黑体辐射规律
斯特潘-玻尔兹曼定律
黑体的辐出度与热力学温度的四次方成正比 \[ M_0(t) = \sigma T^4 \] 斯特潘常量\(\sigma=5.670\times10^{-8}W/(m^2K^4)\)
韦恩移位定律 \[ T\cdot \lambda_m=b,b=2.898\times 10^{-3}m\cdot K \] 当黑体温度升高时,对应于单色辐出度的峰值的波长向短波方向移动
普朗克能量假说
谐振子只能处于某些特定的状态,在这些状态中他们的能量只能是某个能量单元的整数倍
最小的能量单元成为能量子,记为\(\varepsilon\),这些整数倍记为量子数\(n\)
频率为\(\nu\)的谐振子的最小能量单元\(\varepsilon=h\nu,h=6.6260755\times 10^{-34}\)
物体辐射或吸收的能量\(E=n\varepsilon=nh\nu\)
光电效应
光入射到金属表面使电子从金属中脱出的现象称为“光电效应”
特点
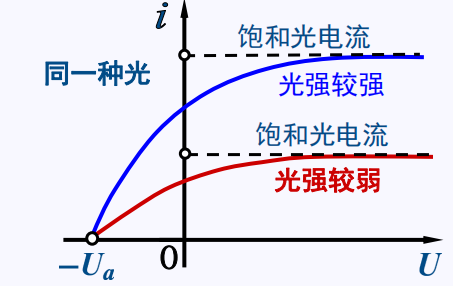
对于同一种光,光强相同时,\(U\uparrow, I\uparrow\)
饱和电流强度与入射光的强度成正比
\(I=0\)时,遏止电压\(U=-|U_a|\)
\(|U_a|\)反映了光电子初动能的大小,光电子初动能为\(\frac{1}{2}m_ev_{max}^2=e|U_a|\)
\[ |U_a|=k\nu-U_0 \]
频率不同的光照射阴极K时,相应的遏制电压也不同
初动能与光强无关,只与入射光的频率有关
只有当入射频率\(\nu\)大于红限频率\(\nu_0\)时,才会产生光电效应,\(|U_a|=k(\nu-\nu_0)\),k是与阴极金属的普适恒量
光电效应具有瞬时性,不到\(10^{-9}s\)即可完成
爱因斯坦的光量子论
一个光子被一个电子所吸收,使电子获得\(h\nu\)能量,一部分用于脱离金属表面做功,一部分成为光电子的初始动能 \[ \frac{1}{2}m_e\nu_{max}^2=e|U_a|=h\nu-h\nu_0 \]
当光照射金属时,电子吸收能量是一次性的,不需要能量积累,电子逸出是瞬间的,无明显时间延迟
光的波粒二象性
波动性:在传播过程中出现干涉、衍射
粒子性:突出表现在与物质相互作用中(光电效应、康普顿效应) \[ \varepsilon=h\nu=mc^2 \]
\[ \Rightarrow p=mc=\frac{h}{\lambda} \]
波尔量子理论
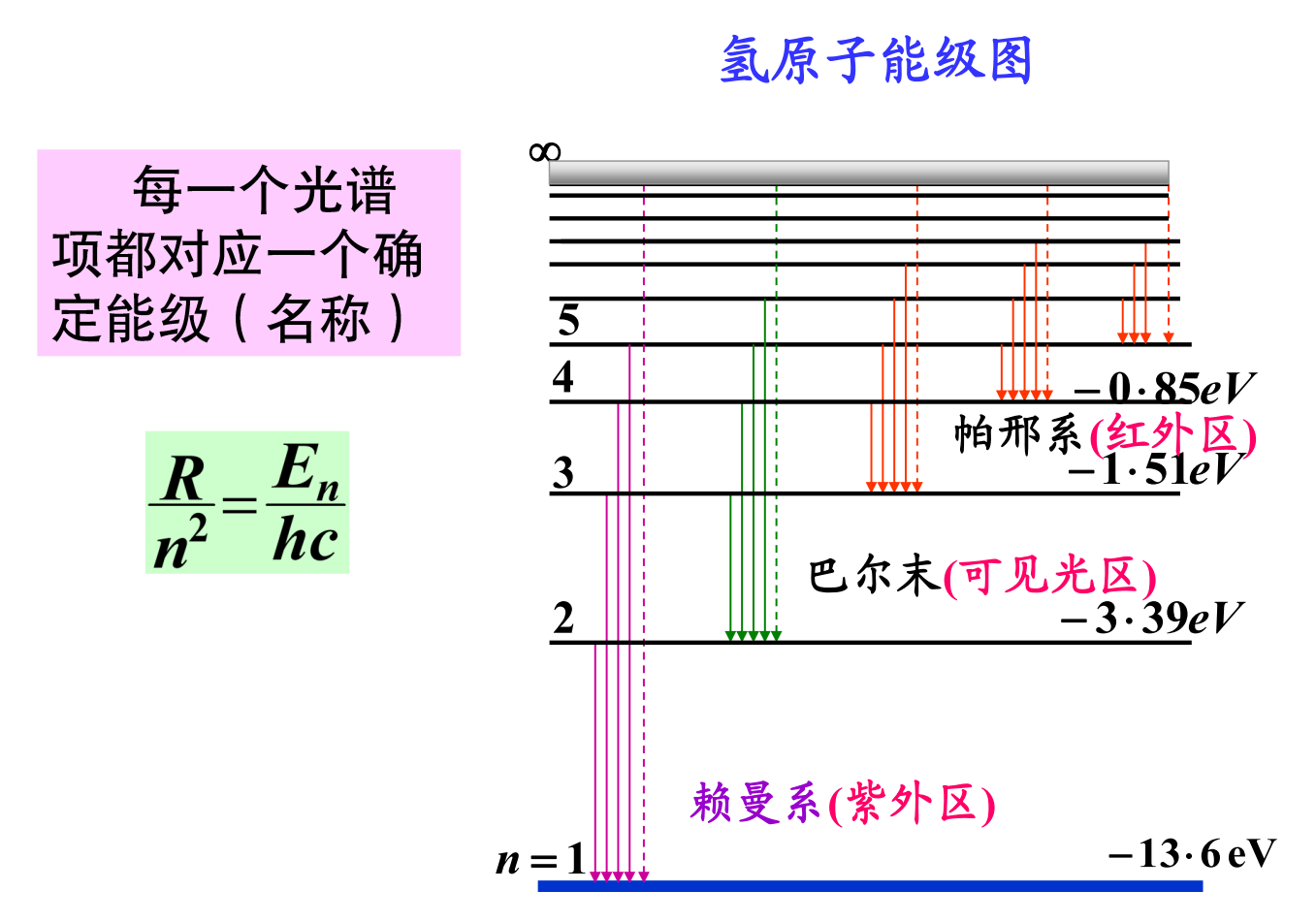
氢原子光谱
巴尔末: \[ \lambda=B\frac{n^2}{n^2-4},n=3,4,5... \] \[ \sigma=\frac{1}{\lambda}=R(\frac{1}{2^2}-\frac{1}{n^2}),n=3,4,5... \]
广义的巴尔末公式/里德伯公式: \[ \sigma=\frac{1}{\lambda}=R(\frac{1}{k^2}-\frac{1}{n^2})=T_k-T_n \] \(k=1,2,3,4...,\ n = k+1, k+2,...,\ R=\frac{4}{B}=1.0973731534\times10^7m^{-1}\)
波尔的氢原子理论
量子化条件:电子以速度\(v\)在半径为\(r\)的圆周上绕核运动时,只有电子的角动量\(L\)等于\(\frac{h}{2\pi}\)的整数倍的那些轨道是稳定的 \[ L=mvr=n\frac{h}{2\pi} \] 跃迁定则:当原子从高能量\(E_n\)的定态跃迁到低能量的\(E_k\)定态时,要发射频率为\(\nu\)的光子 \[ \nu=\frac{E_n}{h}-\frac{E_k}{h} \] 第n个稳定轨道的半径: \[ \left.\begin{matrix} \frac{e^2}{4\pi\varepsilon_0r_n^2}=m\frac{v_n^2}{r_n} \\mv_nr_n=n\frac{h}{2\pi} \end{matrix}\right\}\Rightarrow r_n=\frac{\varepsilon_0h^2}{\pi me^2}n^2\Rightarrow r_n=n^2r_1 \] 波尔半径:\(r_1=0.053nm\)
电子在第n个轨道上运动时,原子的总能量\(E_n\): \[ E_n=\frac{1}{2}m_ev_n^2+(-\frac{e^2}{4\pi\varepsilon_0r_n})=-\frac{1}{n^2}(\frac{m_ee^4}{8\varepsilon_0^2h^2})\\ \Rightarrow E_n=\frac{E_1}{n^2} \] 电子运动的速度: \[ v_n=\frac{e^2}{2\varepsilon_0h}\frac{1}{n},\frac{v_1}{c}\approx \frac{1}{137} \]
波尔理论对氢原子光谱的解释
\[ \left.\begin{matrix} E_n= -\frac{1}{n^2}(\frac{m_ee^4}{8\varepsilon_0^2h^2}) \\\nu=\frac{E_n}{h}-\frac{E_k}{h} \end{matrix}\right\} \Rightarrow \frac{1}{\lambda}=\frac{\nu}{c}=\frac{m_ee^4}{8\varepsilon_0^2h^3c}(\frac{1}{k^2}-\frac{1}{n^2})(n>k) \]
里德伯常数:\(R=\frac{m_ee^4}{8\varepsilon_0^2h^3c}=1.097373\times10^7m^{-1}\)
概念
原子的能量:原子系统处于某状态时所具有的能量
氢原子的状态能量\(\approx\)氢原子中电子的动能 + 核与电子之间的势能
结合能:将动能为零的电子从无限远处移来和一个离子结合成基态的原子所放出的能量
电离能:把某能级的电子搬到无限远处所需要的能量
康普顿效应
实验规律
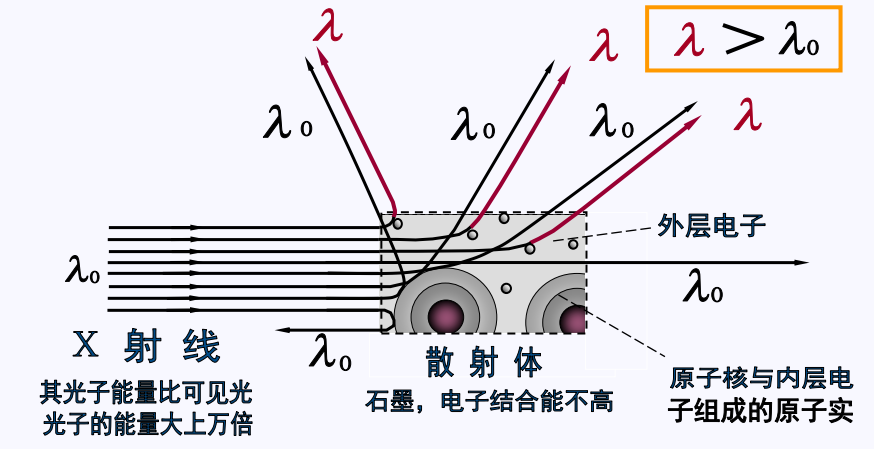
- 散射的射线中有与波长\(\lambda_0\)相同的射线,也有波长\(\lambda>\lambda_0\)的射线
- 散射线波长的该变量\(\Delta\lambda=\lambda-\lambda_0\)随散射角\(\theta\)的增加而增加\(\Delta\lambda=\lambda_c(1-\cos\theta),\lambda_c=2.4263\times10^{-12}m\)
- 同一散射角下波长的改变量相同,与散射物质无关
- 原子量较小的物质,散射较强
实验解释
\(\lambda>\lambda_0\):由于物质中的外层电子的动能远小于入射光子的动能, 碰撞前电子可以看作是静止的。碰撞过程中, 光子的一部分能量传递给电子,能量减小, 频率减小, 因而波长增大。
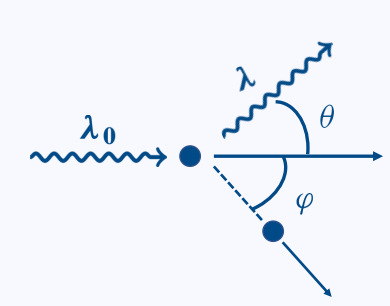
能量守恒: \[ h\nu_0+m_ec^2=h\nu+\frac{m_e}{\sqrt{1-\frac{v^2}{c^2}}}c^2 \] 动量守恒: \[ \left\{\begin{matrix} \frac{h}{\lambda_0}=\frac{h}{\lambda}\cos\theta+\frac{m_e}{\sqrt{1-\frac{v^2}{c^2}}}v\cos\varphi \\ 0=\frac{h}{\lambda}\sin\theta-\frac{m_e}{\sqrt{1-\frac{v^2}{c^2}}}v\sin\varphi \end{matrix}\right. \] 由上述式子相消得: \[ \Delta\lambda=\lambda-\lambda_0=\frac{h}{m_ec}(1-\cos\theta)=\lambda_c(1-\cos\theta),\lambda_c=2.4263\times10^{-12} \] \(\lambda=\lambda_0\):光子与内层电子的碰撞可看作是与原子的碰撞。由于原子的质量远大于光子,碰撞过程中光子的能量几乎不变, 因而波长保持不变。
总结:
原子量较小的物质,电子束缚很弱\(\Rightarrow\)康普顿散射较强
原子量较大的物质,电子束缚很紧\(\Rightarrow\)康普顿散射较弱






