# 磁场与磁介质的相互作用

# 磁场对载流导线的作用

$$\vec{F}=\int_L Id\vec{l}\times \vec{B}$$

两根直流电流的相互作用：

$$F_{12}=\int_LdF_{12}=\int_LI_2d\vec{l}\cdot \vec{B}=\int_a^{a+L\sin \theta}I_2\frac{\mu_0I_1}{2\pi r}\cdot\frac{dr}{\sin\theta}=\frac{\mu_0I_1I_2}{2\pi\sin\theta}\ln\frac{a+L\sin\theta}{a}$$

垂直：

$$F=\frac{\mu_0I_1I_2}{2\pi}\ln\frac{a+L}{a}$$

平行：

$$F=\frac{\mu_0I_1I_2}{2\pi a}$$

# 磁场对载流线圈的作用

磁偶极矩：$$\vec {P_m}=IS\vec {n}，方向：同 I 方向右手定则 $$

线圈总力矩：$$\vec {M}=\vec {P_m}\times\vec {B}$$

# 磁介质

相对磁导率：\mu_r=\frac{B}

# 顺磁质

微观：一个分子电流

未加磁场：$B_0=0,\vec{p_m}\neq0,\sum\vec{p_m}=0$，即每个磁矩均不为 0，但是合磁矩为 0

加磁场：$B_0\neq 0,\sum\vec{p_m}\neq0,\vec{M}=\vec{p_m}\times\vec{B}$，尽量使$\vec{M}=0$

外磁场越强，分子磁矩排列越整齐；磁化电流越大，附加磁场越强。

# 抗磁质

微观：一对分子电流

未加磁场：$B_0=0,\vec{p_m}=\vec{p_{m1}}+\vec{p_{m2}}=0$

加磁场：$\Delta \vec{p_m}$ 的方向与$\vec{B_0}$ 方向永远相反

# 磁化强度

单位体积内分子磁矩的矢量和：$$\vec {M}=\frac {\vec {p_m}}{\Delta V}$$

顺磁质：$\vec{M}$ 与$\vec{B}$ 同向；抗磁质：$\vec{M}$ 与$\vec{B}$ 反向

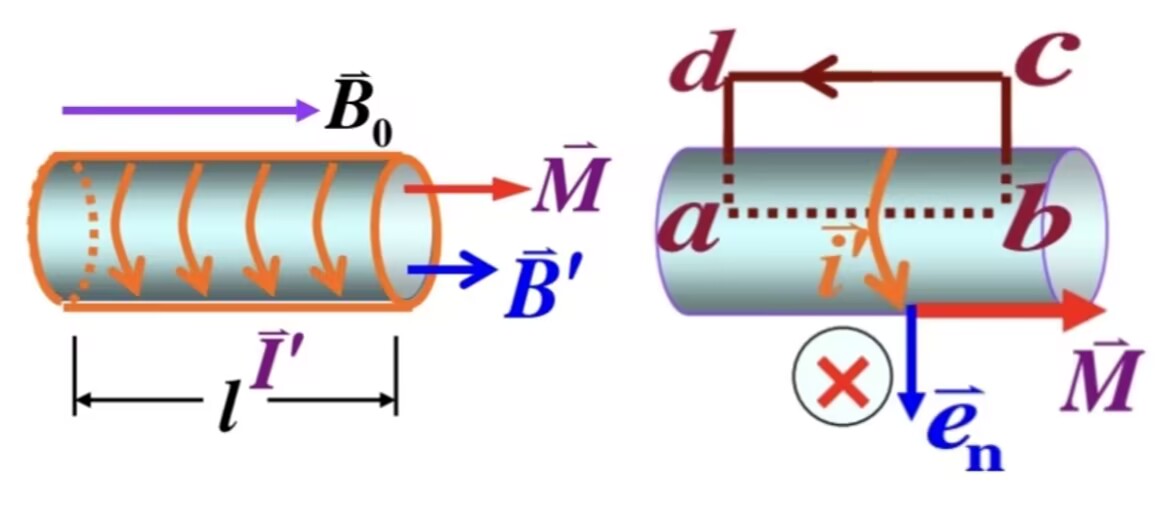
磁化强度的大小等于磁化面电流密度，即$|\vec{M}|=i'$

磁化强度的环流：$\oint_L\vec{M}d{\vec{l}}=i'\cdot \overline{ab}=\sum\limits_{L内}I'$

# 有介质时的高斯定理和安培环路定理

# 高斯定理

$$\oint_S\vec{B}\cdot d\vec{S}=0$$

# 安培环路定理

$$\oint_L\vec{B}d\vec{l}=\mu_0\sum I+\mu_0\sum I'$$

又 $$\oint_L\vec {M}\cdot d\vec {l}=\sum I’$$

$$\oint_L(\frac{\vec{B}}{\mu_0}-\vec{M})\cdot d\vec{l}=\sum I$$

定义磁场强度$\vec{H}$： $$\vec{H}=\frac{\vec{B}}{\mu_0}-\vec{M}$$

安培环路定理：$$\oint_L\vec {H}\cdot d\vec {l}=\sum I$$

磁场强度沿任一闭合路径的环流等于该闭合路径所包围的自由电流的代数和

# 三矢量之间的关系

$$\vec{M}=\chi_m\vec{H},\chi_m\rightarrow介质磁化率$$

$$\vec{B}=\mu_0\mu_r\vec{H},\mu_r=1+\chi_m\rightarrow 相对磁化率$$