离散数学上

集合

• 常见集合：

  N：正整数或自然数集合

  \(N_m\)：\(1,2,...,m\)

  Z：非负整数集合

  \(Z_m\)：\(0,1,2,...,m-1\)

  I：整数集合

  P：素数集合

  C：复数集合

• 寻常集：不包含自身作为元素

  不寻常集：包含自身作为元素

• 基数：集合A中不同元素的个数，记作\(\#A\)

• 幂集：设有集合A，由A的所有子集组成的集合，称为集合A的幂集，记作\(2^A\)，即\(2^A=\left\{S|S \subset A\right\}\)

• 设A是具有基数\(\# A\)的有限集，则\(\#(2^A)=2^{\#A}\)

• 补集：集合A关于全集合U的相对补集称为A的绝对补集，记作\(A'\)

• \(a\in A\)表示a是集合A的一个元素，\(B \subset A\)​表示B是A的一个子集，它意味着B中的每一个元素也是集合A中的元素

  • 若\(A\in B,B\subset C\)，则\(A\in C\) \(\color{red}{（只有这一种组合是对的）}\)
  • \(\color{red}{错错错:}\)
    • 若\(A\in B,B\subset C\)，则\(A\subset C\)
    • 若\(A\subset B,B\in C\)，则\(A\in C\)
    • 若\(A\subset B,B\in C\)，则\(A\subset C\)

• A与B的对称差：集合A、B，由属于A但不属于B以及属于B但不属于A的所有元素构成的集合，记作\(A \oplus B\)，即\(A \oplus B = (A-B)\cup (B-A)\)

• 集合的运算定律

  • 同一律： \(A\cup \varnothing = A\)，\(A \cap U=A\)
  • 互补律：\(A \cup A' = U\)，\(A \cap A' = \varnothing\)
  • 对合律：\((A')' = A\)
  • 等幂律：\(A \cup A = A,A \cap A = A\)
  • 零一律：\(A \cup U = U, A \cap \varnothing = \varnothing\)
  • 吸收率：\(A \cup (A \cap B) = A, A \cap (A \cup B) = A\)
  • 德摩根律：\((A \cup B)' = A' \cap B', (A \cap B)' = A' \cup B'\)

• 对称差运算

  • \(A \oplus B = B \oplus A\)
  • \((A \oplus B)\oplus C = A \oplus (B \oplus C)\)
  • \(A \cap (B \oplus C) = (A \cap B)\oplus (A \cap C)\)
  • \(A \oplus \varnothing =A, A\oplus U = A'\)
  • \(A \oplus A=\varnothing, A\oplus A'=U\)
  • \(A\oplus(A\oplus B)=B\)

• 分划：设\(\pi= \left\{A_i\right\}_{i \in K}\)是集合A的某些非空子集的集合，如果集合A的每个元素在且只在其中之一\(A_i\)中，即如果

  1. 当\(i \neq j\)时，\(A_i \cap A_j = \varnothing\)

  2. \(\bigcup\limits_{i \in K}A_i = A\)

     则称集合\(\pi\)时集合A的一个分划

关系

集合的笛卡尔积

• 序偶：有序二元组

• 笛卡尔积：设\(A_1,A_2,...,A_n\)时、是任意集合，所有有序n元组\((a_1,a_2,...,a_n)\)的集合，称为\(A_1,A_2,...,A_n\)的笛卡尔积，记作\(A_1 \times A_2 \times...\times A_n\)

  即\(A_1 \times A_2 \times...\times A_n = \left\{(a_1,a_2,...,a_n)|a_i \in A_i\right\}\)

• \(A \times B \neq B \times A\)

  \(A \times B = B \times A = \varnothing\)

• \(A \times (B \cup C) = (A \times B) \cup (A \times C)\)

  证明与笛卡尔积有关的定理利用序偶

关系

• 笛卡尔积\(A_1 \times A_2 \times...\times A_n\)的任何一个子集称为\(A_1,A_2,...,A_n\)上的n元关系

• 设\(\rho\)是A到B的一个关系，定义域\(D_{\rho}\)，值域\(R_{\rho}\)

• 逆关系\(\widetilde{\rho} = \left\{(b,a)|(a,b)\in \rho \right\}\)

• 若\(\rho\)是由A到B的一个关系，且\((a,b)\in \rho\)，则称a对b有关系\(\rho\)，记作\(a\rho b\)，

  如果\((a,b)\notin \rho\)，则记作\(a\rho'b\)

• 集合A上的关系：由集合A到A自身的关系

• 普遍关系\(U_A\)：若\(\rho = A^2\)，则称\(\rho\)为A上的普遍关系，即\(U_A = \left\{(a_i,a_j)|a_i,a_j \in A\right\}\)

  恒等关系\(I_A\)：\(I_A=\left\{(a_i,a_i)|a_i \in A\right\}\)

• 复合关系：\(\rho_1 \cdot \rho_2 = \left\{(a,c)|a\in A，c\in C,且\exists b\in B,s.t.(a\rho_1b,b\rho_2 c)\right\}\)

• \((\rho_1 \cdot \rho_2)\cdot \rho_3 = \rho_1 \cdot (\rho_2 \cdot \rho_3)\)

  证明与关系有关的定理利用序偶

关系的表示方法

• 关系矩阵
  • 设\(\rho_1\)是A到B的关系，\(\rho_2\)是B到C的关系，它们的关系矩阵分别为\(M_{\rho_1}、M_{\rho_2}\)，则复合关系\(\rho_1 \cdot \rho_2\)的关系矩阵\(M_{\rho_1 \rho_2}=M_{\rho_1} \cdot M_{\rho_2}\)
  • \(M_{\rho ^n}=M_{\rho}^n\)
• 关系图

集合A上关系的性质和闭包运算

• 设\(\rho\)是集合A上的关系

  • 若对于所有的\(a\in A\)，有\(a\rho a\)，则称\(\rho\)是自反的，否则是非自反的

    若对于所有的\(a\in A\)，有\(a\rho'a\)，则称\(\rho\)是反自反的

  • 对于所有的\(a,b \in A\)，若每当有\(a\rho b\)就有\(b\rho a\)，则称\(\rho\)是对称的，否则是非对称的

    对于所有的\(a,b \in A\)，若每当有\(a\rho b\)和\(b\rho a\)，就必有\(a=b\)，则称\(\rho\)是反对称的，也可描述为对于所有的\(a,b \in A\)，若\(a \neq b\)，则\(a\rho b\)和\(b\rho a\)不能同时出现

  • 对于所有的\(a,b,c \in A\)，若每当有\(a\rho b和b\rho c\)就有\(a\rho c\)，则称\(\rho\)是可传递的，否则，\(\rho\)是不可传递的

• A上关系的性质在关系矩阵上的体现

  • \(\rho\)是自反的：主对角线上的元素全为1
  • \(\rho\)是对称的：关于主对角线对称
  • \(\rho\)是反对称的：对于\(i\neq j\)，若\(r_{ij}=1\)，则\(r_{ji}=0\)

• A上的关系的性质在关系图上的体现

  • \(\rho\)​是自反的：每个结点引出一个单边环
  • \(\rho\)是反自反的：每个结点无单边环
  • \(\rho\)是对称的：对每一由结点\(a_i\)指向结点\(a_j\)的边，必有一相反的边
  • \(\rho\)是反对称的：任何两个不同的借点之间最多有一条边

• 设\(\rho\)是集合A上的关系

  • \(\rho\)的自反闭包\(r(\rho)\)：\(r(\rho)=\rho \cup I_A\)
  • \(\rho\)的对称闭包\(s(\rho)\)：\(s(\rho)=\rho \cup \widetilde{\rho}\)
  • \(\rho\)的传递闭包\(t(\rho)\)：\(t(\rho)=\bigcup_\limits{i=1}^\infty \rho^i\)​（若\(\# A=n\)，则\(t(\rho)=\bigcup _\limits{i=1}^n \rho^i\)）

  \({\color{red}r(\rho)、s(\rho)、t(\rho)分别是集合A上包含\rho最小的自反关系、对称关系、可传递关系}\)

  (可以利用关系图得到传递闭包，只要能到达就有一条线连接)

• 设\(\rho_1\)、\(\rho_2\)是集合A上的关系，且\(\rho_1 \subset \rho_2\)，则\(r(\rho_1) \subset r(\rho_2)\)，\(s(\rho_1) \subset s(\rho_2)\)，\(t(\rho_1) \subset t(\rho_2)\)

集合A上两类重要的关系

等价关系

定义：集合A上的关系\(\rho\)，如果它使自反、对称且可传递的，则称\(\rho\)为A上的等价关系

等价类：

定义：设\(\rho\)是集合A上的等价关系，则A中等价于a的全体元素的集合，成为a所生成的等价类，用\([a]_{\rho}\)表示，即\([a]_{\rho}=\left\{b|b\in A,a\rho b \right\}\)

性质：

1. A中每一个元素生成的等价类非空
2. 彼此等价的元素属于同一个等价类
3. 彼此不等价的元素属于不同的等价类，且这些等价类之间没有公共元素

分划：

定义：设\(\rho\)是集合A上的等价关系，则等价类的集合\(\left\{[a]_{\rho} |a\in A\right\}\)构成A的一个分划

说明：每一个等价类就是一个分化块，因为A的每一元素的等价类（在\(\rho\)下）是唯一的，所以分划也是唯一的，这种由等价关系\(\rho\)的等价类所组成的A的分划，称为A上由\(\rho\)所导出的等价分化，用\(\pi_{\rho}^A\)​​表示

商集：

等价类的集合\(\left\{[a]_{\rho}|a\in A\right\}\)称为A关于\(\rho\)的商集，记作\(A/\rho\)，\(A/\rho\)的基数称为\(\rho\)的秩

\(res_m(i)\)表示用m除以i所得的余数

细分：

如果\(I_2\)的每一个分化块都是\(I_1\)的某一个分化块的子集，则\(I_2\)是\(I_1\)的细分

偏序

偏序定义：集合A上的关系\(\rho\)，如果它是自反、反对称、可传递的，则称\(\rho\)是A上的一个偏序关系，用\(\leq\)表示；显然一个偏序的逆也是偏序，用\(\geq\)表示。

全序定义：一个集合A上的偏序，若对于所有的\(a,b\in A\)，有\(a\leq b\)或\(b \leq a\)，则称它为A上的一个全序。\(\color{red} {集合A中任意两个元素都是可比的}\)

良序定义：一个集合A上的偏序，若对于A的每一个非空子集\(S \subset A\)，在S中存在一个元素\(a_s\)（S中的最小的元素），使得对于所有\(s \in S\)，有\(a_s \leq s\)​，则称它为A上的一个良序。\(\color{red}{集合A中有最小元素}\)

特点：

• 全序或者良序一定是偏序
• 偏序不一定是全序或者良序
• 一个偏序如果是良序则一定是全序

函数

函数

\(A \times B\)的每一个子集都是由A到B的关系，其中一部分子集可以用来定义由A到B的函数，用\(B^A\)表示这些函数的集合，即\(B^A=\left\{f|f:A\rightarrow B\right\}\)，\(\color{red}{当A、B都是有限集}\) \(\color{red}{的时候}\)，\(\#A=m,\#B=n\)，从A到B不同函数共有\(n^m\)，即\(\#(B^A)=(\# B)^{\#A}\)

三种特殊函数

定义：

• 内射：当\(a_i \neq a_j\)时，有\(f(a_i) \neq f(a_j)\)，也就是当\(f(a_i) = f(a_j)\)时，有\(a_i=a_j\)（集合A中的不同元素在B中有不同的像）
• 满射：B中每一个元素都是A中至少一个元素的像
• 双射：集合A和集合B的元素间一一对应

特点：

​ 如果A、B都是有限集

• \(\#A \leq \#B\)时，f有可能时内射
• \(\#A\geq \#B\)​时，f有可能是满射
• \(\#A=\#B\)​时，f有可能是双射

函数的复合

设有函数\(f:A\rightarrow B\)和\(g:B\rightarrow C\)，那么：

1. 如果f和g都是内射，则\(gf\)也是内射
2. 如果f和g都是满射，则\(gf\)也是满射
3. 如果f和g都是双射，则\(gf\)​​也是双射

设有函数\(f:A\rightarrow B\)和\(g:B\rightarrow C\)，那么：

1. 如果\(gf\)是内射，则f是内射
2. 如果\(gf\)是满射，则g是满射
3. 如果\(gf\)是双射，则f是内射，g是满射

逆函数

1. 设函数\(f:A\rightarrow B\)是一个双射，则逆函数\(f^{-1}\)也是一个双射
2. 设函数\(f:A\rightarrow B\)是一个双射，则\((f^{-1})^{-1}=f\)
3. 如果函数\(f:A\rightarrow B\)是可逆的，则有\(f^{-1}f=I_A,ff^{-1}=I_B\)
4. 设有函数\(f:A\rightarrow B\)和\(g:B\rightarrow A\)，当且仅当\(gf=I_A,fd=I_B\)时，有\(g=f^{-1}\)
5. 设有函数\(f:A\rightarrow B\)和\(g:B\rightarrow A\)，且f和g都是可逆的，则\((gf)^{-1}=f^{-1}g^{-1}\)

集合的基数

概念

概念：集合的基数即集合中不同元素的个数

等势：设有集合A、B，如果存在双射函数\(f:A\rightarrow B\)，则说A和B有相同的基数，或者说A和B等势，记作\(A\sim B\)

注：对于有限集来说，A和B有相同的基数指的是它们元素个数相同

有限集：如果集合A与集合\(N_m=\left\{1,2,...,m\right\}\)属于同一基数类，则称集合A是有限集。有限集的基数就是该集合中的元素个数。

可数集：如果集合\(A\sim N\)，则称A为可数集。可数集的基数记作\(\aleph_0\)。 一个集合是可数集的充分必要条件是它全部元素可以排成一个无穷序列的形式。

可计数集：有限集和可数集称为可计数集。

性质

1. 可数集的无限子集仍是可数集

2. 任一无限集A必包含一可数子集

3. 设集A可数，集B有限，且\(A\cap B=\varnothing\)，则\(A\cup B\)可数

4. 若A、B都是可数集，\(A\cap B=\varnothing\)，则\(A\cup B\)​可数

5. 有限个可数集的并是可数集

6. 可数个(互不相交的)可数集的并依旧是可数集

7. 设有集合A，B，若A的子集\(A_1\)和B的子集\(B_1\)，使得\(A\sim B_1,B\sim A_1\)，则\(A\sim B\)

图论

基本概念

概念

• n阶图：有n个结点的图

• (n, m)图：n个结点m条边

  (n, 0)图：零图

  (1, 0)图：平凡图

• 完全图：任意两个不同结点都相邻接的图叫完全图

  补图：由G所有节点和为了使G变成完全图添加的边构成的图

• d次正则图：所有节点都具有同一度d

• 子图：\(\widetilde{V}\) \(\subset\) \(V\), \(\widetilde{E}\) \(\subset\) \(E\)

  真子图：\(\widetilde{V}\) \(\subset\) \(V\), \(\widetilde{E}\) \(\subset\) \(E\) , 且 \(\widetilde{E}\) \(\neq\) \(E\)

  生成子图：\(\widetilde{V}\) \(=\) \(V\) , \(\widetilde{E}\) \(\subset\) \(E\)

• 图的同构：两个图存在边与边之间的双射关系

• 伪图：设 \(G = (V, E)\) , V是一个有限非空集合，E是V中任意元素的非有序对偶的多重集

  • 在E中允许出现相同元素的对偶
  • 在E中无序对偶{\({Vi, Vj}\)}可能出现r次

• 多重图： 没有长度为1的环的伪图

  简单图：没有自环且没有重数大于1的边

• 邻接（结点与结点，边与边）、关联（结点与边）、孤立点、孤立边

性质定理

• 握手定理----在(n, m)图中，\(\sum\limits_{i=1}^{n}\)deg(\(vi\))\(=2m\)​;
• n阶完全图\(Kn\)中，\(m=\)\(\frac{1}{2}\)n(n-1);
• 两个图同构的必要条件：
  1. 它们有相同的结点数和相同的边数
  2. 对应结点的度数相同

路

概念

• 开路、真路、回路、环
  • 没有重复结点的开路是真路
  • 没有重复结点的回路是环
• 短程、距离

性质定理

• 设G是具有结点集\(V={v_1,v_2,...,v_n}\)的图，则对于任意两个相连接的结点\(v_i,v_j \in V (v_i \neq v_j)\)，其短程是一条长度不大于n-1的真路

图的矩阵表示

设\(G = (V, E)\)，其中 \(V = \left\{ v_1, v_2, ..., v_n\right\}\)

• 邻接矩阵\(A = (a_{ij})\)

  \[ a_{ij} =\left\{ \begin{aligned} 1& &{若\left\{ v_i, v_j \right\}} \in E \\ 0& &否则 \end{aligned} \right. \]​

  • 一个图的邻接矩阵是对角线元素均为0的0-1矩阵，反之，一个对角线全为0的0-1矩阵一定可以唯一地做一个图
  • 如果两个图的邻接矩阵可以通过行列变换得到，那么这两个图同构
  • 图G的邻接矩阵A的第i行（或第i列）出现1的个数就是节点\(v_i\)​的度
  • \(A^l (l = 1, 2, 3, ...)\)的\((i, j)\)项元素\(a_{ij}^{(l)}\)是连接\(v_i\)到\(v_j\)长度为l的路的总数

• 关联矩阵\(I = (b_{ij})\)是一个n\(\times\)m矩阵

  \[b_{ij} = \left\{ \begin{aligned} 1& &若v_i和e_j是关联的 \\ 0& &否则 \end{aligned} \right.\]

  • I中每一列都正好包含两个 1，并且任何两个列都是不相同的
  • 第i行中的1的个数即为节点\(v_i\)的度

• 连接矩阵\(C = (c_{ij})\)

  \[c_{ij} = \left\{ \begin{aligned} 1& &若从v_i到v_j存在一条路 \\ 0& &否则 \end{aligned} \right.\]​

  • 当C中所有元素都为1时图是连通 的

图的连通性

概念

• 连通图：如果存在一条路连接\(v_i\)和\(v_j\)，则称结点\(v_i\)与\(v_j\)是连接的，若G中任意两个节点均是连接的，则称图G是连通的

• 割边：如果在图G中删去边\(\left\{v_i, v_j\right\}\)后，图G的分图数增加，则称边\(\left\{v_i,v_j\right\}\)是G的割边

• 割点：如果在图G中删去结点\(v_i\)及与其相关联的边之后，图G的分图数增加，则称结点\(v_i\)是G的割点

• 边割集：设图\(G = (V, E)\)是一连通图，若有E的子集S，使得在图G中删去S中的所有边后，得到的子图G-S变成具有两个分图的不连通图，而删去了S的任一真子集后，得到的子图仍然是连通图，则称S是G的一个边割集

• 点割集：设图\(G = (V, E)\)是一连通图，若有V的子集\(V_1\)使得在图G中删除了\(V_1\)中的所有结点之后，所得到的子图\(G - V_1\)不连通或为平凡图，则称\(V_1\)是G的一个点割集

  （割点是点割集的特例）

• 断集：设\(G = (V, E)\)是一连通图，\(V_1 \subset V\), G中端点分别属于\(V_1\)和\(V_1'\)的所有边的集合，则成为G的断集

  边割集是断集的特例

• 关联集：设v是图\(G = (V,E)\)的一个结点，与v相关联的所有边的集合，称为结点v的关联集，记作\(S(v)\)

• 点连通度：\(K(G) = min\left\{\ \#V_i|V_i是G的点割集\right\}\)，点连通度是为了使G成为一个非连通图需要删除的点的最少数目

• 边连通度：λ\((G) = min\left\{ \# S|S是G的断集\right\}\)，边连通度是为了使G成为一个非连通图需要删去的边的最少数目

性质定理

• 图G中，边\(\left\{v_i,v_j\right\}\)为割边的充要条件是边\(\left\{v_i,v_j\right\}\)不在G的任何环中出现
• 在图G中，结点v为割点的充要条件是存在两个结点u和w，使得连接u和w的所有路中都出现结点v
• 对于一个给定的图\(G = ( V, E)\)，如果能把结点集V分成两个互补的子集\(V\)和\(V'\)，使得同一结点集中的任意两个结点之间，至少存在一条不包含另一个结点子集中的任何结点的路，那么G中的端点分别在\(V_1\)和\(V_1'\)​中的边组成G的一个边割集
• 对于任意的图\(G = (V, E)\)，有\(K(G) \leq \lambda(G) \leq \delta(G)\)（其中\(\delta(G)\)是图G的最小度

欧拉图

概念

• 欧拉回路：在图G中找到一个回路，它通过G的每条边一次且仅一次
• 欧拉路：具有欧拉回路的图
• 欧拉图：通过图G每条边一次且仅一次的开路

性质定理

• 一个连通图G为欧拉图的充要条件是G的每一结点的度均为偶数
• 连通图G具有一条连接结点\(v_i\)和\(v_j\)的欧拉路的充要条件是，\(v_i\)和\(v_j\)​是G中仅有的具有奇数度的结点
• 欧拉回路的边不可以重复但是结点可以重复，所以欧拉回路不一定是环路

哈密顿图

概念

• 哈密顿环：找到一个环它通过图G的每个结点一次且仅一次

  哈密顿路：通过图G每个结点一次且仅一次的开路

  哈密顿图：具有哈密顿环的图

• 闭图：设G是具有n个结点的图，若对于\(deg(u)+deg(v) \geq n\)​的每一对结点u和v，均有u和v相邻接，则称图G是闭图

• 闭包：图G的闭包是一个与G有相同结点集的闭图，记作\(G_c\)，使\(G \subset G_c\)，且异于\(G_c\)的任何图H，若\(G \subset H \subset G_c\)，则G不是闭图

  图G的闭包是包含图G的最小闭图

性质定理

• 图G的闭包是唯一的
• 每个哈密顿图都一定是连通的
• 若图\(G = (V,E)\)是哈密顿图，则对于V的任何一个非空子集S，有\(W(G-S)\leq\#S\)，这里\(W(G-S)\)表示G - S中分图的个数
• 设G是具有n个结点的图，若有结点u和v不相邻接，且\(deg(u) + deg(v) \geq n\)，则当且仅当图\(G+\left\{u,v\right\}\)是哈密顿图时，图G时哈密顿图
• 设有图G当且仅当\(G_c\)​是哈密顿图时，图G是哈密顿图
• 若图G的闭包\(G_c = K_n\)，且\(n \geq 3\)，则G是哈密顿图
• 设图\(G = (V, E)\)，\(\#G \geq 3\)，若V中任意两个不相邻的结点u和v，均有\(deg(u) + deg(v) \geq n\)，则G是哈密顿图
• 设图\(G = (V, E)\)，\(\#V \geq 3\)，若对于任意的\(v \in V\)，均有\(deg(v) \geq \frac{n}{2}\)，则G是哈密顿图

树

概念

• 树：不包含环的连通图

  树林：不包含环的图

  树叶：度为1的结点

• 生成树：若连通图G的生成子图T是一棵树，T是G的生成树

  最小生成树：在所有生成树中有最小权值

• 若G是一\((n,m)\)连通图，G的生成树\(T_G\)是一\((n,n-1)\)图

  环秩：在得到\(T_G\)之前需要删除的边的总数为\(m-(n-1)\)，该数为环秩，环秩是为了“弄破”G的所有环而必须由G中删去的边的最小数目

  弦：被删去的每一条边

  枝：在生成树\(T_G\)中的边

性质定理

• 在\((n,m)\)树中，\(m = n - 1\)

• 具有两个或更多个结点的树至少有两片树叶

• 两个节点之间由唯一的真路连接的图就是树

  \(m=n-1\)的连通图是树

  \(m=n-1\)​且无环的图是树

有向树

概念

• 有向树：一个不包含环的有向图G，若它只有一个结点\(v_0\)入度为0，而所有其它结点入度为1

• 根：节点\(v_0\)

  树叶或终点：出度为0的结点

  级：从\(v_0\)到结点\(v_i\)的距离

• m元树：在一有向树中，若每一个结点的出度都小于或等于m

  完全m元树：若每个结点的出度等于m或0

• 外部结点：树叶结点

  内部结点：分支结点

• 外部路径长度：根到所有外部结点的距离和

  内部路径长度：根到所有内部结点的距离和

  树的路径长度：根到所有结点的距离和

• 有序树：规定了每一级上结点的次序，一般规定同一级结点的次序为从左到右

• 前缀码：在一个序列的集合中，如果没有一个序列是另一个序列的前缀，则称该序列的集合为前缀码

• 最优树：一颗带权\(W_1,W_2,...,W_t\)的二元树，如果在所有带权\(W_1,W_2,...,W_t\)的二元树中具有最小的权，则称为最优树

性质定理

• 一颗二元树第i级的最大结点数是\(2^i\)，高度为h的二元树的最大结点数为\(2^{h+1}-1\)​
• 设T为一颗完全二元树（T不为孤立结点）有r个内部结点，内部路径长度为I，外部路径长度为E，则\(E=I+2r\)
• 设T为一颗二元树，有\(n_0\)个叶节点，\(n_2\)个出度为2的结点，则\(n_2=n_0-1\)
• 设T是一颗完全二元树，有n个结点，\(n_0\)个叶节点，则\(n=2n_0-1\)
• 设T是一颗完全m元树，有\(n_0\)个叶节点，t个分支结点，则\((m-1)t=n_0-1\)

二部图

概念

• 二部图：若一个图G的结点集V能分成两个子集\(V_1\)和\(V_2\)使得\(V_1 \cup V_2=V\),\(V_1 \cap V_2 = \varnothing\)，使得G的每一条边\(\left\{V_i,V_j\right\}\)的端点\(v_i \in V1, v_j \in V_2\)，则称图G是一个二部图

  完全二部图：如果\(V_1\)的每一个结点和\(V_2\)的每一个结点想邻接，则G为完全二部图

• 匹配：设G是具有互补结点子集\(V_1\)和\(V_2\)的二部图，其中\(V_1=\left\{v_1,v_2,...,v_q\right\}\)，\(V_1\)对\(V_2\)的匹配是G的一个子图，它由q条边\(\left\{v_1,v_1'\right\},\left\{v_2,v_2'\right\},...,\left\{v_q,v_q'\right\}\)组成，其中\(v_1',v_2',...v_q'\)是\(V_2\)中q个不同的元素

性质定理

• 图G为二部图的充要条件是至少有两个节点，它的所有回路均为偶数长
• 二部图存在\(V_1\)对\(V_2\)的匹配的必要条件是\(\# V_2 \geq \#V_1\)
• 二部图存在\(V_1\)对\(V_2\)的匹配的充要条件是\(V_1\)中每k个结点至少和\(V_2\)​中k个结点相邻接
• 二部图存在\(V_1\)对\(V_2\)的匹配的充分条件是，存在某一整数\(t>0\)使
  1. 对\(V_1\)中每个结点，至少有t条边与其相关联
  2. 对\(V_2\)中每个结点，至多有t条边与其相关联

平面图

概念

• 平面图：能画于平面上而无任何交叉

性质定理

• 平面图的欧拉公式：设G是一连通的平面图，则有\(n-m+k=2\)这里的n、m、k分别是图G的结点数、边数、面数（包括无限面）
• 有两条或者更多条边的任何连通的平面图G中,有\(m \leq 3n-6\)
• 

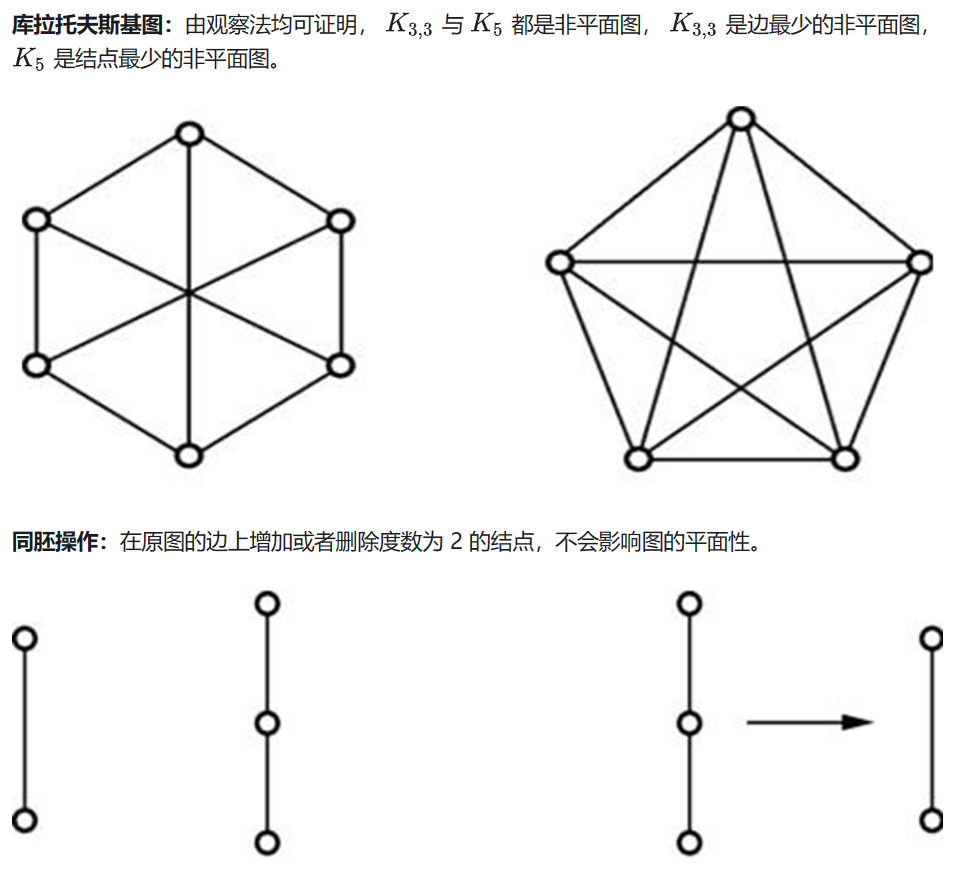
有向图

概念

• 弱连通：看作无向图时是连通的

  单向连通：任何两个结点\(v_i\)和\(v_j\)中至少有一个由另一个出发是可达的

  强连通：任何两个结点\(v_i\)和\(v_j\)都是相互可达的

  强连通的有向图是单向连通的，单向连通的有向图是弱连通的

• 强分图、单向分图、弱分图分别是G的极大连通子图、极大单向连通子图、极大弱连通子图

性质定理

• 一个连通的有向图具有欧拉回路的充要条件是，G的每一个结点的入度和出度相等

  一个连通的有向图具有欧拉路的充要条件是，除了两个结点外，G的每一个结点的入度和出度相等