光波基础

相位差\(\Delta \phi\)和光程差\(\delta\)： \[ \Delta \phi=\frac{2\pi}{\lambda}\delta \] 光强与振幅的平方成正比： \[ I\propto E^2 \]

光强的合成 \[ I=I_1+I_2+2\sqrt{I_1I_2}\overline{\cos\Delta\phi} \]

杨氏双缝

条纹特点：明暗相间，等间距，直条纹

光程差 \[ \delta = \frac{x\cdot d}{D}=\begin{cases} k\lambda& 明纹\\ (2k+1)\frac{\lambda}{2}&暗纹 \end{cases} \] 条纹左边 \[ x_{明}=\frac{k\lambda D}{d}\\ x_{暗}=\frac{(2k+1)\lambda D}{2d} \]

条纹间距 \[ \Delta x=\frac{D}{d}\lambda \] 光程差每改变\(\lambda\)，条纹移动一级 \[ (n −1)l = \Delta k\cdot \lambda \]

等倾干涉

光程差 \[ \delta=2n_2d\cos\gamma(+\frac{\lambda}{2})=2d\sqrt{n_2^2-n_1^2\cdot\sin^2i}(+\frac{\lambda}{2}) \] 条纹间隔分布： \[ (\Delta \gamma)_{\Delta k=1}=\frac{\lambda}{2n_2d\sin\gamma} \]

中心为亮斑
条纹级次k，内高外低；中央条纹级次最高
条纹内疏外密
厚度增加时，中心冒出亮斑，周围亮斑不断向外扩大

等厚干涉

光程差 \[ \delta=2nd(+\frac{\lambda}{2}) \]

劈尖干涉

相邻条纹对应的厚度差 \[ \Delta d=\frac{\lambda}{2n} \] 相邻明（暗）纹间距 \[ l=\frac{\Delta d}{\sin \theta}\approx \frac{\Delta d}{\theta}=\frac{\lambda}{2n\theta} \]

牛顿环

\[ r^2\approx 2Rd\\ \]

\[ r=\begin{cases} \sqrt{\frac{(2k-1)R\lambda}{2}}& k=1,2,3... \\ \sqrt{kR\lambda} &k=0,1,2... \end{cases} \]

中心为暗纹
愈往边缘，级次越高
中心疏，旁边密
平凸透镜向上平移时，空气膜的厚度增大，与 \(d_k\)对应的厚度向中心移进，干涉牛顿环向中心逐渐缩进

迈克尔逊干涉仪

M2平移\(\Delta d\)，等厚干涉条纹移过N条 \[ \delta=2\Delta d=N\lambda\\ \Delta d=N\frac{\lambda}{2} \]

相干长度&相干时间

相干长度： \[ L = \frac{\lambda^2}{\Delta \lambda} \] 相干时间： \[ \tau =\frac{L}{c} \] 转换公式： \[ \Delta \lambda = -\frac{\lambda^2}{c}\Delta\nu \]

单缝衍射

单缝衍射光强

\[ I=I_0(\frac{\sin\alpha}{\alpha})^2,\alpha=\frac{\pi a\sin\theta}{\lambda} \]

单缝衍射光强分布特点

\(\theta\)角相同处光强相同
中央主极大：\(\theta=0\)处，\(I=I_0=I_{max}\)
极小（暗纹）：\(I=0\Rightarrow \sin\alpha=0\) \[ a\sin\theta=\pm k\lambda(k=1,2,3...) \]
次极大：\(\frac{dI}{d\alpha}=0,\frac{d^2I}{d\alpha^2}<0\)

\[ \alpha=\pm 1.43\pi,\pm2.46\pi,\pm3.47\pi,... \]

\[ a\sin\theta=\pm 1.43\lambda,\pm2.46\lambda,\pm3.47\lambda,... \]

\[ a\sin\theta=\pm(2k+1)\frac{\lambda}{2}(k=1,2,3,...) \]
光强分布曲线

\(I\)次极大<<\(I\)主极大
明条纹宽度

中央明纹：\(k=\pm1\)两暗纹之间的范围：\(-\frac{\lambda}{a}<\sin \theta<\frac{\lambda}{a}\)（\(\frac{\lambda}{a}\)称为半角宽度）

其他明纹：\(k,k+1\)两条暗纹之间的范围：\(\frac{\lambda}{a}<\sin \theta<\frac{2\lambda}{a}\)

条纹的影响

缝宽改变 \[ \Delta x\propto\frac{1}{a} \] 缝宽越小，条纹展的越开，衍射作用愈显著

缝宽越大，条纹向中央明纹靠拢，衍射作用愈不显著

波长改变 \[ \Delta x\propto \lambda \] 波长越长，条纹宽度越宽，衍射效果越明显

白光入射，不同波长的光的明纹不完全重叠；中央O为白色明纹，近O为紫色，最远为红色

半波带法

缝可以分成几个半波带：确定光程差\(\delta=a\sin\theta\)，\(\delta\)包含多少个\(\frac{\lambda}{2}\)就分成几个半波带
相同的\(\theta\)，分成半波带的面积一样大；不同的\(\theta\)，分成半波带的面积不一样大（半波带面积\(\propto\)衍射明纹亮度）

\(\theta\)越大，\(\delta\)越大，包含的\(\frac{\lambda}{2}\)多，分成半波带数目多，一个半波带面积小
半波带法中，暗纹位置精确成立，明纹位置近似成立

巴俾涅原理

在点光源照射下，一个不透光物体产生的衍射图样和一个带有与该物体形状、大小完全相同的孔的衍射屏产生的衍射图样完全相同。

双缝衍射

双缝衍射光强

\[ I=I_0(\frac{\sin\alpha}{\alpha})^2(\frac{\sin(2\beta)}{sin\beta})^2 \]

\[ \alpha=\frac{\pi a\sin\theta}{\lambda},\beta=\frac{\pi (a+b)\sin\theta}{\lambda} \]

双缝衍射图样特点

中央明纹：\(\theta=0,I=I_0\)，为单缝光强的4倍
光强极大 \[ (a+b)\sin\theta=\pm k\lambda(k={\color{red}{0}},1,2,...) \]
缺项，同时满足： \[ (a+b)\sin\theta=\pm k\lambda(k=0,1,2,...)--双缝干涉加强，明纹 \] \[ a\sin\theta=\pm k' \lambda(k'=1,2,...)--单缝衍射相消，暗纹 \]

计算得缺项条件： \[ \frac{\beta}{\alpha}=\frac{a+b}{a}=\frac{k}{k'} \]

光栅衍射

光栅：大量等宽等间距的平行狭缝（或反射面）构成的光学元件。

光栅常数：透光部分的宽度a（缝宽）与不透光部分的宽度b之和

光强公式： \[ I=I_0(\frac{\sin\alpha}{\alpha})^2(\frac{\sin(N\beta)}{sin\beta})^2\\ \alpha=\frac{\pi a\sin\theta}{\lambda},\beta=\frac{\pi (a+b)\sin\theta}{\lambda} \]

光栅衍射特点

主极大 \[ \beta=k\pi(k=0,\pm 1,\pm 2,...)时,在d\sin \theta=k\lambda出现主极大 \]
暗纹位置 \[ \beta=(k+\frac{m}{N})\pi时(m = \pm1, \pm2,...\pm N-1),在d\sin \theta=(k+\frac{m}{N})\lambda出现极小值 \]
- 相邻两主极大之间有\(N-1\)条暗纹，\(N-2\)个次极大
- 其他位置的光强比主极大小得多
主极大半角宽 \[ 第k级主极大：d\sin\theta_k=k\lambda \]

\[ k级主极大旁边最近的暗纹：d\sin(\theta_k+\Delta \theta)=(k+\frac{1}{N})\lambda \]

\[ {\large \mathbf{k级主极大半角宽：\Delta\theta =\frac{\lambda}{Nd\cos\theta_k}} } \]
斜入射的光栅方程 \[ 主极大：d(sin\phi+\sin\theta)=\pm k\lambda \]

\[ 缺级：a(\sin\phi+\sin\theta)=\pm k'\lambda, \ d(\sin\phi+\sin\theta)=\pm k\lambda \]

色散

光栅的色散本领：将不同波长的光在谱线上分开的本领。只反映谱线主极大中心分离的程度，但不能说明谱线是否重叠，因为谱线本身是有宽度的。

角色散： \[ D=\frac{\Delta\theta_k}{\Delta \lambda}\\ 因为d\sin\theta_k=k\lambda,D=\frac{k}{d\cos\theta_k} \] 线色散： \[ D_l=\frac{\Delta l_k}{\Delta \lambda}=f\frac{\Delta\theta_k}{\Delta \lambda} \]

与光栅缝数N无关
减少d，选择更高级次k的光谱，可增大角色散本领

光栅的分辨本领R：恰能分辨的两条谱线的平均波长\(\lambda\)与它们的波长差\(\delta\lambda\)之比。表征着分辨清楚两条谱线的能力 \[ R=\frac{\lambda}{\Delta\lambda}=Nk \]

布喇格公式

天然晶体可以看做是光栅常数很小的空间三维衍射光栅。

原子在晶体中按晶格点阵排列，晶体由一系列平行的原子层（晶面）所组成。

入射波被原子散射

同一晶面上（点间干涉）：同一江面上相邻原子散射的光波的光程差为0，相干加强

\[ 相邻原子散射x射线干涉极大条件：\delta=bc-ae=h(\cos\theta-\cos\theta')=n\lambda,\ n=0,1,2,...\\ 零级主极大：\theta=\theta' \]
不同晶体上（面间干涉）

若要满足原子散射光相干加强，必须满足： \[ \delta=NM+MP=k\lambda,\ k=1,2,3,...\\ 即：2d\cdot\sin\theta=k\lambda \]

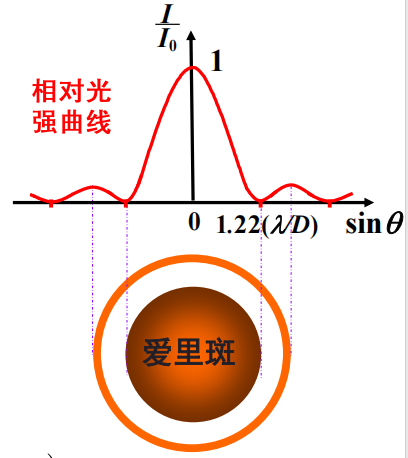
圆孔衍射

衍射第一极小： \[ D\sin\theta_1\approx 1.22\lambda \] 中央亮斑的角半径： \[ \theta_1=\sin^{-1}( 1.22\frac{\lambda}{D})\approx1.22\frac{\lambda}{D} \] 爱里斑半径： \[ R\approx f\theta_1=1.22\frac{f\lambda}{D} \]

光学仪器的分辨率

能够区分两个物点的最小距离，是光学仪器的重要性能

瑞利判据

对于两个等光强的非相干物点，点物\(S_1\)的爱里斑中心恰好与另一个点物\(S_2\)的爱里斑边缘（第一衍射极小）相重合时，恰可分辨两物点

最小分辨角\(\delta\phi\) \[ \delta\phi=1.22\frac{\lambda}{D} \] 分辨率R \[ R=\frac{1}{\delta\phi}=\frac{D}{1.22\lambda} \] 最小分辨距离\(\Delta x\) \[ \Delta x=u\delta \phi \]

人眼

设人眼瞳孔直径为D，玻璃体折射率为n‘ \[ \delta\phi'=\frac{1.22\lambda'}{D}=\frac{1.22\lambda}{n'D}\\ \delta\phi=n'\delta\phi' \] \(\delta\phi\)为眼外两个恰可分辨的物点对瞳孔中心所张的角，称为眼外最小分辨角

显微镜

显微镜的分辨本领用最小可分辨间距来衡量 \[ \delta y=\frac{0.61\lambda}{n\cdot\sin u} \] 其中，n是物所在处介质的折射率，u是物镜半径对物点的张角，\(n\cdot\sin u\)称为物镜的数值孔径，简写为\(N.A.\)

偏振

纵波没有偏振，横波有偏振

光偏振状态

线偏振光

\[ E_x=E\cos\alpha \]

\[ E_y=E\sin\alpha \]

自然光 \[ E_x=E_y \] \[ I_0=I_x+I_y \]

\[ I_x=I_y=\frac{1}{2}I_0 \]

圆偏振光

可分解为两束振动方向垂直，振幅相等，相位差为\(\frac{\pi}{2}\)线偏振光

椭圆偏振光

可分解为两束振动方向垂直，振幅不相等，相位差一定\((0\sim\pi)\)的线偏振光

部分偏振光

马吕斯定律

入射线偏振光的光振动方向与检偏器透振方向的夹角为\(\alpha\) \[ I=I_0\cos^2\alpha \]

布儒斯特定律

当自然光入射到两种介质的分界面上时，反射光和折射光都是部分偏振光

当入射角\(i\)满足\(\tan i=\frac{n2}{n1}\)时

反射光与折射光相互垂直
反射光只有垂直于入射面的光振动
折射光为平行分量多的部分偏振光

光线以入射角\(\gamma\)从\(n_2\)入射 \[ \tan\gamma=\frac{n1}{n2} \]

玻璃堆

反射所获得的线偏振光仅占入射自然光总能量的7.4%，绝大部分垂直分量和全部平行分量都折射到介质中

增强了反射光的强度
增加了折射光的偏振程度

双折射

晶体对光的双折射现象

各向同性介质

各向异性介质

概念

晶体的光轴

沿此方向\(o,e\)光的速度相同，\(n_e,n_o\)也相同，不发生双折射，只要平行于此方向就满足上述条件

晶体的主截面

光轴+晶面法线

光线主平面

光轴+晶体内光线，光轴与\(o(e)\)光构成的平面叫做\(o(e)\)主平面

光轴在入射面时，o光和e光主平面重合，此时o光振动和e光振动互相垂直
一般情况下\(o,e\)主平面夹角很小，可近似认为两者振动垂直

正晶体&负晶体

惠更斯原理

\(o\)光子波面：各方向速度相同，波面——球面

\(e\)光子波面：各方向速度不同，波面——旋转椭球面

平行光轴上：\(v_e=v_o\)，两波面在光轴方向相切

垂直光轴上： \[ \left\{\begin{matrix} v_e<v_o& 正晶体\\ v_e>v_o& 负晶体 \end{matrix}\right. \]

惠更斯作图法

波晶片

表面与光轴平行的晶体薄片

相位差： \[ \Delta\phi=\frac{2\pi}{\lambda}(n_o-n_e)d \left\{\begin{matrix} \Delta \phi<0& 正晶体\\ \Delta \phi>0& 负晶体 \end{matrix}\right. \] 常用波晶片： \[ \left\{\begin{matrix} \frac{1}{4}波片：(n_o-n_e)d=\pm\frac{\lambda}{4}\rightarrow\Delta\phi=\pm\frac{\pi}{2} \\ \frac{1}{2}波片：(n_o-n_e)d=\pm\frac{\lambda}{2}\rightarrow\Delta\phi=\pm\pi \end{matrix}\right. \]

圆偏振光和椭圆偏振光的获得

两互相垂直振动可合成圆或椭圆运动

一束线偏振光经\(\frac{1}{4}\)晶片后，出射光是两束传播方向相同、振动方向相互垂直、频率相等、相位差为π/2的线偏振光。

振幅关系

\[ A_o=A\sin\alpha \]

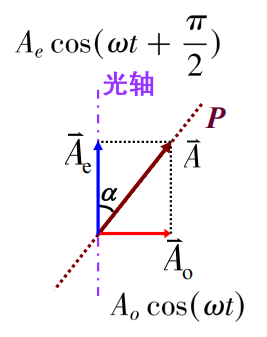
\[ A_e=A\cos\alpha \]

圆偏振光 \[ \alpha=45^o\rightarrow A_o=A_e \]
与e光对应的线偏光 \[ \alpha=0^o\rightarrow A_o=0,A_e=A \]
与o光对应的线偏光 \[ \alpha=90^o\rightarrow A_o=A,A_e=0 \]
椭圆偏振光 \[ \alpha\neq 0^o，45^o,90^o，其他情况下都是椭圆偏振光 \]

偏振光的鉴别

用一块偏振片和一块\(\frac{\lambda}{4}\)波片去鉴别：自然光、部分偏振光、线偏振光、圆偏振光、椭圆偏振光

先利用偏振片
- 光强不变 \(\Rightarrow\) 自然光或圆偏振光
- 光强改变 \(\Rightarrow\) 部分偏振光或椭圆偏振光
再利用\(\frac{\lambda}{4}\)波片及偏振片

在判别”椭圆偏振光“时，先利用偏振片使椭圆的长轴（或短轴）与波片的光轴重合

偏振光的干涉

振幅

经过晶片C： \[ A_o=A_1\cos \alpha\\ A_e=A_1\sin\alpha \] 经过偏振片2，偏振方向P2 \[ A_{e2} = A_e\cos \beta\\ A_{o2} = A_o\sin\beta \] 相位差

经过晶片C： \[ |\Delta\phi_c|=\frac{2\pi d}{\lambda}|n_e-n_o| \] 经过P2后： \[ |\Delta\phi|=\frac{2\pi d}{\lambda}|n_e-n_o|+ \left\{\begin{matrix} \pi& A_{e2}和A_{o2}方向相反 \\ 0& A_{e2}和A_{o2}方向相同 \end{matrix}\right. \]